Hippocrates van Chios

Op de Dag van de Wiskunde (19 november 2011) aan de Kulak in Kortrijk 
gaven Riggy Van de Wiele en Jef De Langhe een erg gewaardeerde uiteenzetting
over de geschiedenis van de wiskunde aan de hand van GeoGebra. Je vindt de volledige tekst in bijlage.
In deze tekst staan ook de bewijzen van enkele merkwaardige stellingen
uit de vlakke meetkunde die je hieronder op mijn blog terugvindt.

In hun exposé hadden ze het ook over de kwadratuur van de cirkel.
In een poging om dit probleem op te lossen slaagde Hippocrates van Chios (470 - 410 v. Chr.) er in
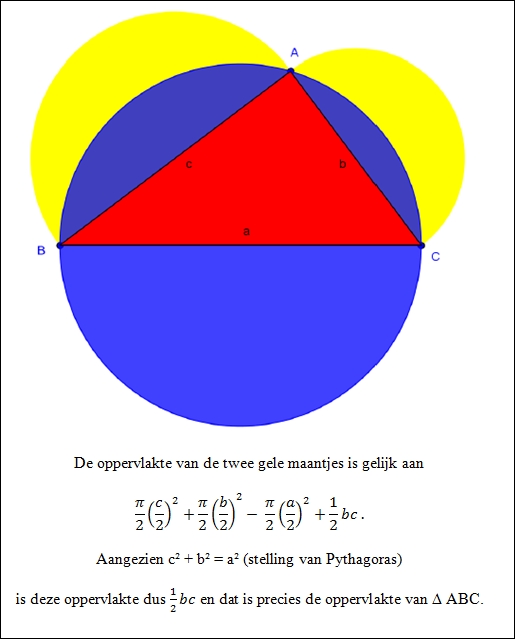
te bewijzen dat de som van de oppervlakten van de twee gele maantjes
op de onderstaande figuur gelijk is aan de oppervlakte van de rode rechthoekige driehoek ABC.
Het kort bewijs maakt gebruik van de stelling van Pythagoras en staat onder de figuur vermeld.

 Als je dit bewijs gesnapt hebt, dan dagen we je uit de onderstaande meerkeuzevraag

uit de JWO-competitie van 2008 op te lossen.

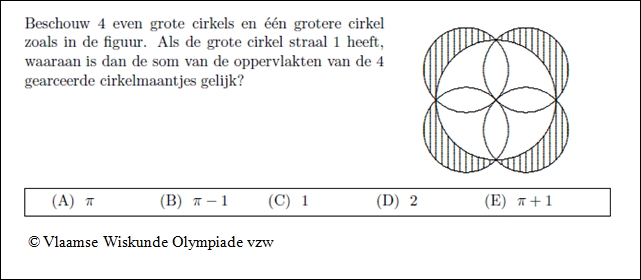
Voor wie er niet direct aan uit geraakt, hebben we de oplossing in bijlage gestopt.

Bijlagen:
oplossing JWO-vraag maantjes van Hippocrates.pdf (154.5 KB)   
WW5 Geschiedenis van de wiskunde met geoGebra.pdf (3 MB)   

Hippocrates van Chios was een Griekse wiskundige die leefde rond 430 v. Chr.
Hij schreef een invloedrijk werk Stoicheia over meetkunde
en het is vrijwel zeker dat Euclides zich hierop baseerde voor zijn eigen meetkundeboeken (Elementen).

Op de onderstaande figuur staat een opgave die een variatie geeft 
op de eigenschap van de maantjes van Hippocrates.

Vanuit het hoekpunt A van een rechthoekige driehoek ABC
laat men de loodlijn neer op de zijde [AB].
H is het voetpunt van deze loodlijn.
Met de middens van de zijden [AB], [AC], [BC], [AH], [BH] en [CH]
tekent men vijf cirkels zoals op de figuur.
Toon aan dat de som van de oppervlakten van de vier maantjes A₁ + A₂ + A₃ + A₄
gelijk is aan de oppervlakte van driehoek ABC.

Hint.  A₁ + A₃ = opp. Δ ABH .

Lukt het?

10-05-2013 om 00:00 geschreven door Luc Gheysens  

De Engelse wiskundige John Wallis (1616-1703) gebruikte in zijn werk Arithmetica infinitorum (1656)
voor het eerst het symbool ∞ voor oneindigheid.

Dit symbool heeft de vorm van een lemniscaat (Grieks: λημνίσκος, band, lint). 
 Deze wiskundige kromme werd beschreven doorvoorgesteld door Jakob Bernoulli
 in een artikel in zijn Acta Eruditorum (1694)
en wordt daarom ook de lemniscaat van Bernoulli genoemd.

Zoals je op de bovenstaande figuur kunt zien
bestaat er een mooie constructiemethode (bijvoorbeeld met GeoGebra) voor deze kromme.
Vertrek van twee cirkels met als middelpunt (2,0) en (-2,0) met als straal 2√2.
Deze cirkels gaan dan ook door (0,2) en (0,-2).
Neem daarna een variabel punt op beide cirkels
zodat het lijnstuk dat die twee punten verbindt de constante lengte 4 heeft.
De meetkundige plaats van het midden van dat lijnstuk zal dan de lemniscaat bepalen.



De lemniscaat van Bernouilli is ook de meetkundige plaats van de punten P
waarvoor geldt dat het product van de afstanden tot twee vaste,
vooraf bepaalde punten F₁ = (-a,0) en F₂ = (a,0) gelijk is aan a²:

10-05-2013 om 00:00 geschreven door Luc Gheysens  

Eeuwen geleden reeds waren de Griekse wiskundigen
en de volgelingen van Pythagoras in het bijzonder
in de ban van de gehele getallen.

 Zo onderzochten ze de eigenschappen van de zogenaamde veelhoeksgetallen (figuurlijke of figuratieve getallen).
De bekendste soorten zijn de driehoeksgetallen en de vierhoeksgetallen (kwadraten).
Hieronder staan naast deze twee soorten ook de vijf- en zeshoeksgetallen afgebeeld.
Uiteraard is er van elke soort een oneindig doorlopende rij getallen.

Maar wist je dat er een algemene formule bestaat voor het n-de p-hoeksgetal G(n,p)?

06-05-2013 om 00:00 geschreven door Luc Gheysens  

Claudius Ptolemaeus van Alexandrië (87 - 150 na Chr.)
was een begaafde sterrenkundige, wiskundige, geograaf en muziektheoreticus.

Met zijn epicykeltheorie verklaarde hij o.a. waarom de planeten
soms een schijnbare retrograde (achteruitgaande) beweging maakten aan het firmament.
Volgens deze theorie volgen de planeten cirkelvormige banen
waarbij het middelpunt van de cirkel zelf beweegt op een grotere cirkel (de deferent).
In feite waren de planetenbanen volgens deze theorie dus epicycloïden.

Ptolemaeus berekende ook een degelijke benadering voor pi, nl. 377/120 ≈ 3,1416...

Voor de wiskundigen blijft hij echter vooral bekend door een merkwaardige stelling (lees de bijlage!)

Hieronder staat een mooie opgave die een toepassing is op de stelling van Ptolemaeus.

Kan je dit bewijzen?

Bijlagen:
Stelling van Ptolemaeus - klassiek bewijs (Dick Klingens).pdf (171.1 KB)   

CURIOSUM MATHEMATICUM

Af en toe duikt er in de wiskunde een eenvoudige eigenschap van getallen op.
In 1939 ontdekte Dov Juzuk de volgende verrassende eigenschap.

Schrijf de natuurlijke getallen in volgorde onder elkaar op
in groepjes van 1, 2, 3, 4 ... getallen en te beginnen met het getal 1.
Schrap dan de rijen met een even volgnummer.
Dan blijkt de som van de getallen in de eerste n resterende rijen telkens gelijk te zijn aan n⁴.

 Voor wie hierdoor wat in de war is: een bewijs door volledige inductie zit in bijlage.

Bijlagen:
Curiosum Mathematicum - bewijs.pdf (196.4 KB)   

Op de voorbije finale van de Vlaamse Wiskunde Olympiade (editie 2013)
kregen de deelnemers een mooie oefening uit de vlakke meetkunde voorgeschoteld.

Beschouw (in het vlak) drie concentrische cirkels met stralen 1, 2 en 3 en een gelijkzijdige driehoek
zodanig dat op elk van de drie cirkels één hoekpunt van deze driehoek ligt.
Bereken de lengte van de zijden van deze driehoek.

© Vlaamse Wiskunde Olympiade v.z.w.

UITDAGING. Los deze opgave op met behulp van het computerprogramma GeoGebra.


www.geogebra.org

In de bijlage vind je een verrassende oplossing voor het probleem
die gebruik maakt van de omgekeerde stelling van Ptolemaeus.

Bijlagen:
Oplossing VWO-finalevraag 2013.pdf (277.6 KB)   

WISKUNDE BIJ DE GOUDSMID

Een goudsmid heeft een ketting gemaakt die bestaat uit 
18 karaat gouden ringetjes met verschillende afmetingen.
Er zijn ringetjes van drie verschillende formaten in verwerkt.
De goudsmid beweert dat de drie soorten ringetjes dezelfde hoeveelheid goud bevatten
(d.w.z. dezelfde oppervlakte hebben) omdat de koorden [AB], [CD] en [EF] dezelfde lengte hebben.

Heeft de goudsmid gelijk?

Tip. De stelling van Pythagoras toepassen.
Antwoord in bijlage

Bijlagen:
WISKUNDE BIJ DE GOUDSMID - oplossing.pdf (59.2 KB)   

NIEUWE (?) EIGENSCHAP VAN ZEVEN EN DERTIEN


Niet enkel in sprookjes komt het cijfer 7 af en toe voor
maar ook in de wiskunde blijkt het aantrekkelijke eigenschappen te bezitten.

We vermelden hier een nieuwe (?) eigenschap
waarvoor we in bijlage ook een bewijs geven.

Zoek een getal van 6 cijfers dat deelbaar is door 7.
We beweren dat elk getal dat je bekomt
via een cyclische permutatie van de cijfers van dat getal
ook weer deelbaar is door 7.

Voorbeeld. 
364 175 = 7 x 52 025.



Via cyclische permutatie bekom je dan
641 753 = 7 x 91 679
417 536 = 7 x 59 648
175 364 = 7 x 25 052
753 641 = 7 x 107 663
536 417 = 7 x 76 631.

Uit het bewijs (zie bijlage) volgt dat deze eigenschap ook geldig is voor het priemgetal 13.
Zo is 635 921 = 13 x 48 917.
Controleer nu zelf eens dat de getallen
359 216, 592 163, 921 635, 216 359 en 163 592
ook weer deelbaar zijn door 13. 

Test nu zelf eens of de eigenschap geldig is
voor een getal van 3 cijfers dat deelbaar is door 37.

Bijlagen:
EIGENSCHAP VAN 7.pdf (166.2 KB)   

MIJN UURWERKPARADOX



Om ongeveer 5 voor 12 en 5 na 12
maken de grote en de kleine wijzer van een uurwerk een hoek van 30°.
Hoeveel keer maken de twee wijzers dan elke dag
tussen middernacht en 12 uur 's middags een hoek van 30°?

Een simpele redenering is de volgende.
Ongeveer om 00.05 uur is er voor de eerste keer een hoek van 30° tussen beide wijzers.
Daarna is er rond elk uur telkens 2 keer een hoek van 30°
(ongeveer om 00.55 uur en ongeveer om 1.05 uur,
ongeveer om 2.05 uur en ongeveer om 2.15 uur enzovoort ...).
Ongeveer om 11.55 uur is er voor de laatste keer een hoek van 30°.
Dit geeft in totaal 1 + (11 x 2) + 1 = 24 keer.

Waar zit de fout in deze redenering?

28-04-2013 om 00:00 geschreven door Luc Gheysens  

Bestaat er een verband tussen de getallen pi en phi?



In de bijlage bewijzen we de volgende formule:





Verrassend toch ?
Pi is immers geen oplossing van een vierkantsvergelijking met gehele coëfficiënten
(pi is een transcendent irrationaal getal) terwijl phi dat wel is (phi is een algebraïsch irrationaal getal).



PI en PHI: om van te genieten!

Bijlagen:
Een merkwaardig verband tussen pi en phi.pdf (164.2 KB)   

Archimedes' Laboratorium is een boeiende en uitdagende website
die elke maand een wiskundig probleem lanceert.
Zie: http://www.archimedes-lab.org/ bij de rubriek 'Monthly Puzzle'.

We troffen er een ogenschijnlijk eenvoudige puzzel aan 
die ook een simpele en creatieve oplossing heeft.

PUZZEL 131
G is een willekeurige punt binnen een gelijkzijdige driehoek ABC.
Projecteer G loodrecht op de drie zijden en verbind G met de drie hoekpunten.
Dan ontstaan zes driehoeken (figuur 1).
Toon aan dat de som van de oppervlakten k + m + o
gelijk is aan de som van de oppervlakten l + n + p.

  Figuur 1

BEWIJS.
Trek door G een evenwijdige met de drie zijden van driehoek ABC.
De driehoek wordt dan verdeeld in drie parallellograms en drie gelijkzijdige driehoeken.
De lijnstukken die G met de hoekpunten A, B en C verbinden
verdelen deze parallellograms en deze gelijkzijdige driehoeken
telkens in twee delen met dezelfde oppervlakte.
Dan is
k + m + o = (x + a) + (y + b) + (z + c)
= (a + y) + (b + z) + (c + x) = l + n + p.

Q.E.D.

Figuur 2

24-04-2013 om 00:00 geschreven door Luc Gheysens  

KETTINGBREUKEN

Een kettingbreuk is één van die zonderlinge vondsten waarover men zich als wiskundige kan verbazen.

Een kettingbreuk is in feite een breuk in een breuk in een breuk in een breuk...
Er verschijnt telkens een breuk met teller 1
en in de noemer een geheel getal vermeerderd met een breuk met als teller 1
en dit herhaalt zich steeds weer.

Elk irrationaal getal is te schrijven als een oneindig lange kettingbreuk.

Zo ziet de kettingbreuk voor het getal π er uit:

En er bestaan ook nog een andere voorstellingen
waarin de kwadraatgetallen op een verrassende manier opduiken:

En dit is de kettingbreuk voor het getal φ (gulden snede):

In 2010 promoveerde Ionica Smeets (één van de wiskundemeisjes) aan de Universiteit van Leiden
via een doctoraatsthesis 'On continued fraction algorithms'.
Je vindt de tekst in bijlage.
Op p. 109-111 lees je hoe je zelf de kettingbreuk voor pi
(of een ander iarrtionaal getal) kunt vinden.
Meteen een leuke oefening voor in de wiskundeles!

Bijlagen:
Thesis Ionica Smeets - Kettingbreuken.pdf (5.5 MB)   

Ontdek jouw leerstijl

David A. Kolb is een gerespecteerd leerpsycholoog en pedagoog
die o.a. een studie maakte over de leerstijlen van leraars.
Hij kwam hierbij tot de conclusie dat er vier grote leerstijlen kunnen afgebakend worden:
er zijn doeners, dromers, denkers en beslissers.


Op http://www.123test.nl/leerstijl/ 
kan je via een eenvoudige test te weten komen
tot welk type jij behoort.
Zeker eens doen!

Zelf blijk ik tot het type 'denker' te behoren.
Wellicht typisch voor heel veel wiskundigen ...

 

In het tijdschrift BREEDBEELD van het VVKSO
verscheen deze maand een artikel
van de hand van collega Geert Delaleeuw en mezelf
waarin we o.a. verwijzen naar de diverse leerstijlen.
Het volledige artikel
met 7 tips voor de leerlingen
en 7 tips voor de leraar
voor het verwerven van wiskundige competenties
vind je in bijlage.
Met dank aan hoofdredacteur en collega Marleen Lippens.


Info en abonnementen: http://ond.vvkso-ict.com/vvksomainnieuw/document.asp?DocID=2442

Het is belangrijk jouw leerlingen te kennen
maar wellicht is het even belangrijk te weten wie je zelf bent!

Bijlagen:
Wiskunde in BREEDBEELD.pdf (1.6 MB)   

Regelmatige patronen en symmetrische figuren
oefenen vaak een magische aantrekkingskracht uit op wiskundigen.

Een mooi voorbeeld hiervan is een enneagram
(uit het Grieks: ennea is negen en gramma is tekening).
Via een regelmatige negenhoek stelt men in de pseudo-psychologie negen mogelijke persoonlijkheidstypes voor
en de pijlen ertussen symboliseren de onderlinge interactie tussen deze karaktertypes.

De negen types verhouden zich in een gestructureerde wijze tot elkaar.
Als iemand ontspannen en effectief is (in veilige omstandigheden)
neemt hij de goede eigenschappen van een bepaald ander type over (in de onderstaande figuur tegen de pijlen in)
en als iemand juist gespannen is (in stressvolle omstandigheden)
neemt hij de slechte eigenschappen van weer een ander type over (met de pijlen mee).

Op http://www.locomotiva.nl/test.php
kan je via een test ontdekken tot welk type jij behoort.

Hieronder zie je het resultaat van de test die ik vandaag zelf heb afgelegd...

Wist je dat ...
men een regelmatige negenhoek niet correct kan construeren 'op de Griekse wijze', d.w.z. met passer en liniaal
... en dat een regelmatige zevenhoek de veelhoek is met het kleinste aantal zijden waarvoor dit niet lukt ?

Een fraai resultaat over regelmatige veelhoeken is de volgende stelling:

Neem op een cirkel met straal 1 n punten die de cirkel in n bogen met dezelfde lengte verdelen.
Verbind één van de punten met de overige n-1 punten.
Dan is het product van de lengtes van deze n-1 koorden gelijk aan n.

In bijlage vind je een bewijs waarbij we gebruik maken van complexe getallen.

Bijlagen:
Stelling over een regelmatige n-hoek.pdf (206.7 KB)   

DE VLAG VAN TOGO

Als men twee vlaggen van de Afrikaanse republiek Togo 
 naast elkaar ophangt zoals op de bovenstaande afbeelding
dan blijken de punten A, B en C op één rechte lijn te liggen.

Wat betekent dat dan voor de verhouding van de lengte tot de breedte van deze vlag?

Via de stelling van Thales komen we tot een merkwaardig besluit:

De verhouding van de lengte tot de breedte van de vlag van Togo
is precies gelijk aan het getal  φ van de gulden snede (met φ ≈ 1,618).

Op wikipedia vonden we de juiste afmetingen van die vlag:
lengte = 80,9 cm en breedte = 50 cm en 80,9 : 50 = 1,618. 

15-04-2013 om 00:00 geschreven door Luc Gheysens  

Vandaag 15 april zet de doodle van Google Leonhard Euler (1707-1783) in de kijker.
Deze veelzijdige en geniale wiskundige werd op 15 april in Bazel geboren.

De doodle verwijst o.a. naar het feit dat Euler de basis legde voor de grafentheorie
via het gekende probleem van de 7 bruggen van Königsberg,
naar de formule e^{i x} = cos x + i sinx
en naar de formule V – E + F = 2
die een verband legt tussen het aantal hoekpunten (V = Vertices),
het aantal ribben (E = Edges) en het aantal zijvlakken (F = Faces)
van een willekeurig convex veelvlak.

Wie zich wil verdiepen in de grafentheorie
vind in bijlage de cursus van collega Fabien Decruyenaere (met dank!)
die op de voorbije Dag van de Wiskunde in Kortrijk hierover een lezing gaf.

Wie meer houdt van veelvlakken
dagen we uit om de volgende twee problemen op te lossen.

         

Welke van de 4 figuren op de linkse afbeelding is de ontvouwing van een kubus?
En welke van de 4 figuren op de rechtse afbeelding is de ontvouwing van het afgebeelde prisma?
Bron: New Puzzle Quizzes Deluxe (app)

Bijlagen:
Grafen naar grafen - syllabus.pdf (211.4 KB)   

 
Een perfect of volmaakt getal is een natuurlijk getal
dat gelijk is aan de som van zijn delers, het getal zelf niet meegerekend.

De kleinste twee volmaakte getallen zijn 6 en 28:
6 = 1 + 2 + 3 en 28 = 1 + 2 + 4 + 7 + 14.

Vermoedelijk maakten de oude Egyptenaren al studies van perfecte getallen.
Het is bekend dat Pythagoras perfecte getallen onderzocht.
Perfecte getallen hadden in die tijd een religieuze status.
In de beginjaren van het christendom bijvoorbeeld was er een theorie
dat de getallen 6 en 28 door God gekozen waren als perfecte getallen:
6 is het aantal dagen waarin God de aarde had geschapen
en 28 het aantal dagen waarin de maan om de aarde draait.
De heilige Augustinus (354-430) schreef ooit:
Zes is geen perfect getal omdat God de aarde in zes dagen geschapen heeft,
maar God heeft de aarde in zes dagen geschapen omdat zes een perfect getal is.
Bron: wikipedia.

In de Elementen van Euclides (boek IX, proposite 36) duikt een verrassende stelling
die een verband geeft tussen volmaakte getallen en priemgetallen:
Als 2ⁿ – 1 een priemgetal is, dan is 2^n-1(2ⁿ  –  1) een volmaakt getal.
Bewijs in bijlage.


Om de betekenis van deze stelling te begrijpen
volstaat het sommen van opeenvolgende machten van 2 (2⁰ = 1, 2¹ = 2, 2² = 4 ...) te bekijken:
 
1 + 2 = 3 is een priemgetal en daarom is 3 x 2 = 6 een volmaakt getal.
1 + 2 + 4 = 7 is een priemgetal en daarom is 7 x 4 = 28 een volmaakt getal.
1 + 2 + 4 + 8 = 15 is geen priemgetal en 15 x 8 = 120 geen volmaakt getal.
1 + 2 + 4 + 8 + 16 = 31 is een priemgetal en daarom is 31 x16 = 496 een volmaakt getal.

Kan je nu zelf het vierde volmaakt getal vinden?


 

Bijlagen:
Volmaakte getallen en priemgetallen - bewijs stelling.pdf (194.8 KB)   

HELIX EN CYCLOÏDE




Een helix (schroeflijn) ontstaat wanneer een punt
een eenparige cirkelbeweging uitvoert
in combinatie met een eenparige rechtlijnige beweging
in een richting die daar loodrecht op staat.



Een cycloïde ontstaat wanneer een punt beweegt op een cirkel
die rolt zonder glijden over een horizontale rechte lijn.

In een artikel dat verscheen in de Nieuwe Wiskrant
wijst Martin Kindt op een mooi verband tussen beide krommen.
De cycloïde (vlakke kromme) blijkt namelijk een projectie te zijn van de schroeflijn (ruimtekromme).
Lees hiervoor het artikel in bijlage.

Bijlagen:
Helix en cycloIde - Martin Kindt.pdf (21.6 KB)   

Het Wiskundetijdschrift Pythago­ras is onlangs begon­nen met een Face­bookpa­gina.

Op deze pagina zijn o.a. te vinden:
- Kleine Nootjes: wekelijks een uitdagend wiskundepuzzeltje
- Opgaven uit de Pythagoras-Olympiade
- Samenvattingen van artikels uit Pythagoras
- Wiskundenieuwtjes
- Lezersrubriek: bijdrage van leraars en docenten (bv. GeoGebra-constructies).

Facebookpagina: http://www.facebook.com/Pythgrs?ref=hl

            Pythagoras: verdraaid leuk!

PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

Kan je dit nootje kraken?

BROERS EN ZUSSEN

De moeder van David en Susan is in verwachting van een baby.
Als het een meisje is, heeft David tweemaal zoveel zussen als broers.
Maar als het een jongetje is, dan heeft Susan tweemaal zoveel broers als zussen.

Hoeveel kinderen heeft moeder (zonder het kind waarvan ze in verwachting is)?

PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

14-04-2013 om 00:00 geschreven door Luc Gheysens