|
Vanaf september 2009 werkt men in het eerste jaar van de
eerste graad A-stroom met een nieuw leerplan wiskunde.
Vanaf september 2010 komt het ook in voege in het
tweede jaar.

Een belangrijk aandachtspunt in het nieuwe leerplan is het probleemoplossend denken.
Het aanbieden van 'het probleem van de week' kan
een attractieve manier zijn om de leerlingen hun wiskundekennis te laten
toepassen.
De uitgeverijen van wiskundehandboeken schenken hieraan
zeker voldoende aandacht
en ook de vragen van de Kangoeroewedstrijd
komen hiervoor in aanmerking.
Je vindt de vragen van de Wallabie-editie 2009 voor de
eerste graad in bijlage.
Meer informatie tref je aan op www.wiskundekangoeroe.be,
waar je ook oefenopgaven vindt van de voorbije edities.
De leerplancommissie stelde een nuttig document beschikbaar met een overzicht
van de parate kennis en vaardigheden in
de 1ste graad.
Je vindt het in wordformaat in bijlage.
Een ander aandachtspunt in het nieuwe leerplan is het functioneel ICT-gebruik.
Met het dynamisch meetkundeprogramma GeoGebra is er heel wat mogelijk.
De constructie van de rechte van Euler in een willekeurige driehoek (zie onderstaande
figuur)
is wellicht de meest uitdagende oefening voor een leerling
van de eerste graad.
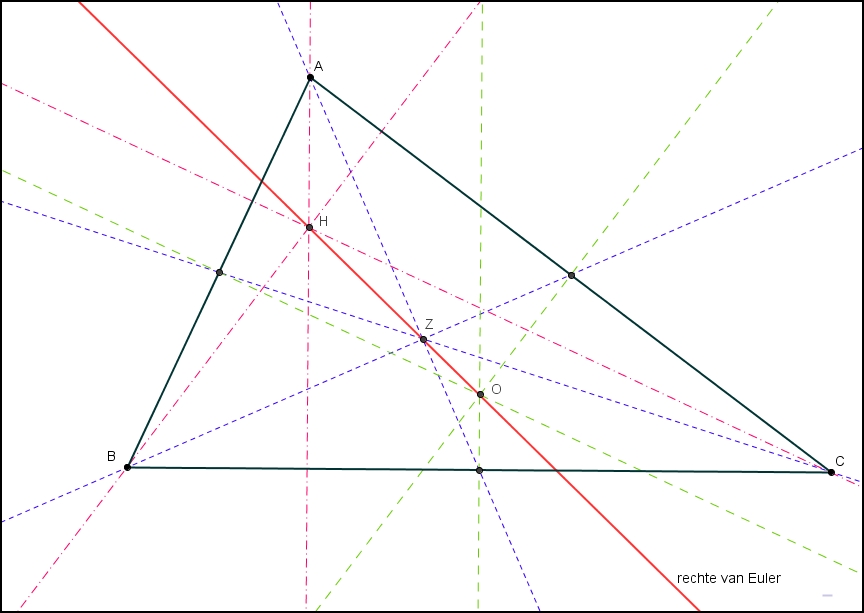
Als je deze GeoGebra-figuur zelf tekent, kan je de hoekpunten van driehoek ABC verslepen
en vaststellen dat het hoogtepunt H, het middelpunt van de omgeschreven cirkel O en het zwaartepunt Z
steeds op één rechte liggen (de rechte van Euler) en dat |HZ| = 2|ZO|.
Zelf maakte ik deze constructie voor het eerst in 1966 onder de hoede
van mijn gedreven wiskundeleraar Frans Vandendriessche in het toenmalige Sint-Jozefinstituut in Kortrijk.
Frans gaf er meer dan 40 jaar les en leerde generaties studenten rekenen met gehele getallen, met rationale getallen en met lettervormen.
Hij leerde ze op een systematische manier vergelijkingen en vraagstukjes met één onbekende oplossen.
Hij leerde ook aan hoe men met passer en liniaal nauwkeurige meetkundige constructies kan maken
en hoe men een meetkundige stelling bewijst.
In mijn verdere carrière zou ik dan ook verschillende bewijzen voor deze enig mooie stelling van Euler optekenen.
In bijlage vind je twee eenvoudige bewijzen voor deze enig mooie stelling.
Het eerste maakt gebruik van een homothetie en het tweede
steunt op vectorrekenen.

Bijlagen:
De rechte van Euler - bewijs.pdf (109.7 KB)
Vademecum eerste graad A-stroom.doc (1.3 MB)
wallabie_2009.pdf (372.3 KB)
29-06-2009 om 00:00
geschreven door Luc Gheysens 
|
