EEN BOEKENRAADSEL

Sidonie heeft een luxe-editie van de avonturen van Suske en Wiske aangekocht.
De reeks bevat 15 delen en de boeken zijn ook genummerd van 1 tot en met 15.
Op een zekere dag stelt haar man Lambik iets bijzonders vast.
De boeken blijken in een merkwaardige volgorde te staan,
want de som van de nummers van elke twee opeenvolgende boeken
is een kwadraatgetal (1, 4, 9, 16 of 25).

Kan jij vinden in welke volgorde de 15 boeken gerangschikt staan?

Tip. Bij de getallen 8 en 9 past telkens slechts één ander getal
zodat de som een kwadraatgetal is.

Oplossing in bijlage.

Bijlagen:
Boekenraadsel - oplossing.pdf (81.6 KB)   

HOGERE WISKUNDE

Wiskundigen zijn altijd op zoek naar veralgemeningen
en ontdekken zo soms merkwaardige objecten.
We stellen er hier twee voor die thuis horen in de rubriek 'hogere wiskunde'.

DE HYPERKUBUS

De hyperkubus of vierdimensionale kubus is een object
dat je uiteraard in onze driedimensionale ruimte niet zult tegenkomen
maar dat in de fantasie van de wiskundigen wel bestaat.

Als je een lijnstuk (eendimensionaal object) in een richting die er loodrecht op staat
evenwijdig met zichzelf verplaatst, creëer je een vierkant.
Als je een vierkant (tweedimensionaal object) in een richting die er loodrecht op staat
evenwijdig met zichzelf verplaatst, creëer je een kubus.
Als je dan een kubus (driedimensionaal object) in een richting die er loodrecht op staat
evenwijdig met zichzelf verplaatst, creëer je een hyperkubus.

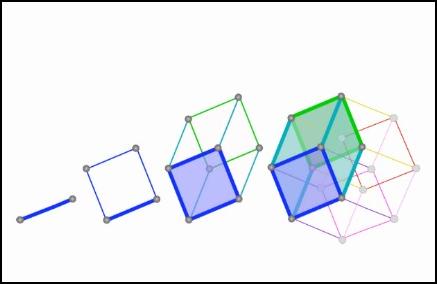
Een lijnstuk heeft 2 hoekpunten (eindpunten),
een vierkant heeft er 4, een kubus heeft er 8
en een hyperkubus heeft er 16.

Zoals een vierkant een 2D-projectie is van een kubus,
zo is een kubus een 3D-projectie van een hyperkubus.
Misschien snap je hiermee wat je hieronder ziet?

 Driedimensionale projectie van een roterende vierdimensionale kubus.

HET VLAK VAN FANO

Wiskundigen gaan ervan uit dat een vlak in alle richtingen oneindig doorloopt.
Ook een rechte bevat een oneindig aantal punten en is onbegrensd.
Daarnaast bestaat er in de fantasie van de wiskundigen ook iets als een eindige meetkunde.

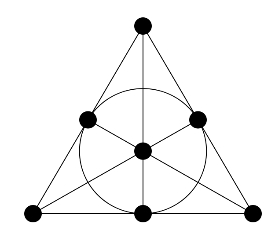
Gino Fano, een Italiaanse wiskundige (1871 - 1952) werkte de eindige meetkunde uit
van het zogenaamde Fano-vlak, dat bestaat uit 7 punten en 7 rechten.
De onderstaande figuur is een model voor het Fano-vlak.
Het is even wennen aan de idee dat ook 'de cirkel' op deze figuur een rechte voorstelt!
Voor de coördinaten van de punten kan je niet werken met de reële getallen,
maar moet je je 'binair beperken' tot 0 en 1.
De 7 punten hebben dan ook een stel binaire coördinaten:
001, 010, 011, 100, 101, 110, en 111.
Door elk punt gaan drie rechten en op elke rechte liggen drie punten.

Het Fano-vlak is het projectieve vlak 
met het kleinste aantal punten en rechten.

28-06-2013 om 00:00 geschreven door Luc Gheysens  

28 JUNI = TAU-DAG ?



De tegenstanders van de pi-dag (3,14 > 3de maand, 14de dag) hebben er niets beter op gevonden
dan 28 juni uit te roepen tot tau-dag (6,28 > 6de maand, 28ste dag).
De Griekse letter τ komt overeen met onze letter t
en verwijst naar de eerst letter van het woord 'toer' (Grieks: τορνος).
1τ = 2π komt dan overeen met een hoek van 360° of één volledige 'toer'.

Er is nog een tweede reden waarom men de letter tau heeft gekozen.
De Griekse letter τ heeft als het ware één been terwijl π er twee heeft
en dat verwijst meteen weer naar 1τ = 2π.

Er zijn ook in de wiskunde en in de wetenschappen heel veel formules waarin de constante 2π voorkomt.
Daarin zou men volgens de aanhangers van de tau-dag 2π moeten vervangen door τ.
Meer hierover lees je in de bijlage 'The Tau Manifesto'.

Zelf blijf ik aanhanger van de pi-dag 
als is het maar omwille van het feit dat ik gemakkelijker
een pi-droedel kan opstellen dan een tau-droedel!

Kan je deze vier oplossen?
Zie ook: http://glorieuxronse.classy.be/droedels.html .



 





Voor wie het niet direct ziet zitten: oplossingen in bijlage!

Bijlagen:
The Tau Manifesto.pdf (617.3 KB)   
VIER PI-DROEDELS.pdf (84.6 KB)   

HET DROSTE-EFFECT

Het Droste-effect is een visueel effect, waarbij een afbeelding een verkleinde versie van zichzelf bevat.
Voor de verkleinde afbeelding geldt weer hetzelfde, enzovoort.
Dit proces van zelfverwijzing heet recursie. In theorie kan dit oneindig doorgaan.

Het effect is vernoemd naar Droste, een producent van cacao en de afbeelding dook voor het eerst op in 1904.
Op de cacaoblikken was een verpleegster afgebeeld die een dienblad droeg
met daarop hetzelfde blik cacao, waarop dan weer hetzelfde stond, enzovoort.

Dit effect werd o.a. door Escher toegepast in zijn grafische kunstwerken.
 Meer hierover lees je op http://escherdroste.math.leidenuniv.nl/
Recursie treedt uiteraard ook op in fractalen.
 Hieronder zie je dit effect bij de Sierpinski-fractal.



Op de onderstaande foto zie je me samen met collega-vakbegeleider Geert Delaleeuw
en Lies Van de Wege, die me opvolgt bij de vakbegeleiding wiskunde van DPB-Brugge.
Ze houdt blijkbaar deze foto vast waarop wij samen staan afgebeeld en creëert zo het Droste-effect!

25-06-2013 om 00:00 geschreven door Luc Gheysens  

DE BAKSTEEN VAN EULER

Leonhard Euler formuleerde ooit het volgende schijnbaar eenvoudige probleem:
bestaat er een balk waarvan de lengte, de breedte en de hoogte een gehele waarde hebben
en waarvan ook de lengte van de zijvlaksdiagonalen een geheel getal is?

Dit is een zogenaamd Diofantisch probleem,
waarbij men een stelsel van drie vergelijkingen moet oplossen
en waarbij de oplossingen gehele getallen moeten zijn:

x² + y² = a²
x² + z² = b²
y² + z² = c².

Het was een zekere Paul Halcke die in 1719 als eerste een oplossing vond voor dit probleem.
Voor x = 44, y = 117 en z = 240 is a = 125, b = 244 en c = 267.
Dit kan men controleren met behulp van de stelling van Pythagoras.

Ga eens na dat dit ook het geval is bij de balken met de volgende afmetingen:
1) x = 85, y = 132, z = 720
2) x = 160, y = 231, z = 792
3) x = 240, y = 252, z = 275
4) x = 140, y = 480, z = 693.

Tot op heden is er echter nog niemand in geslaagd de perfecte balk te vinden
waarbij ook de lengte d van de lichaamsdiagonalen een geheel getal is.
Dit levert een bijkomende vergelijking op : x² + y² + z² = d².

Zin om hier even op te zoeken?

24-06-2013 om 00:00 geschreven door Luc Gheysens  

KANTELENDE VEELHOEKEN

Op de bovenstaande figuur zie je hoe een regelmatige vijfhoek ABCDE
vier keer na elkaar over een hoek van 72° wordt gekanteld
(een rotatie over een hoek van 72° met als centra
van de rotatie achtereenvolgens de punten E, F, G en H).
De vijfhoek rolt dus als het ware over een rechte lijn.
Het punt A komt zo achtereenvolgens in de posities P, Q, R en S terecht.

Wat blijkt nu (via een controle met GeoGebra)?
De oppervlakte van de vijfhoek APQRS
is precies drie maal de oppervlakte van de vijfhoek ABCDE.

Hieronder zie een 'bewijs zonder woorden' van P. Mallinson
voor een kantelende regelmatige tienhoek.
Merk op dat de oppervlakte van elk (roze) driehoekje
dat boven de (rode) veelhoekige lijn uitsteekt
gelijk is aan de oppervlakte van een (wit) driehoekje onder deze veelhoekige lijn.
Hierdoor klopt dit bewijs!

Het leuke aan dit verhaal is dat hieruit volgt dat
de oppervlakte onder één boog van een cycloïde
precies gelijk is aan drie maal de oppervlakte van de cirkel
die deze cycloïde genereert.

 

In de bijlage berekenen we deze oppervlakte op de klassieke manier
met behulp van de integraalrekening.

Bijlagen:
Berekening van de oppervlakte onder een cycloïde.pdf (160.7 KB)