Volgens Wikipedia zijn Sangaku of San Gaku (算額; lett. wiskundige tablet)  Japanse puzzels
die in kleur op houten tafels werden geschilderd gedurende de zogenaamde Edoperiode (1603-1867).
Die tafels werden dan op het terrein van tempels en Shinto-kapellen  opgehangen
als offers aan de goden of als uitdagingen voor de leden van de congregatie.
Men kan sangaku dus beschouwen als 'stellingen zonder woorden' uit de vlakke euclidische meetkunde.
Het bewijs ervan werd meestal niet gegeven.
Veel van de tafels gingen verloren gedurende de periode van modernisering na de Edoperiode,
maar men kent er nu ongeveer negenhonderd die hebben overleefd.

Op de website http://www.wasan.jp/english/  staat een kaart van Japan met de voornaamste vindplaatsen van sangaku.

Een typisch probleem, gepresenteerd op een tafel uit 1824 in de prefectuur Gunma,
gaat over de relatie tussen drie elkaar rakende cirkels met een gemeenschappelijke raaklijn (zie figuur bovenaan deze pagina).

Als de stralen van de twee buitenste cirkels resp. r₂ en r₃ zijn en de straal van de middelste kleine cirkel r₁ dan is het te bewijzen dat

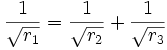
Voor wie op zoek is naar een bewijs hiervan, verwijzen we naar de bijlage.

 Op het internet kan men een groot aantal van deze mooie en uitdagende sangaku vinden,
maar het bewijs ervan vraagt vaak heel wat parate kennis van vlakke euclidische meetkunde.
Kijk bijvoorbeeld eens op http://www.cut-the-knot.org/pythagoras/Sangaku.shtml .
Het Nederlands tijdschrift Pythagoras besteedde de voorbije jaren bijzondere aandacht aan sangaku
en via hun webshop (www.pythagoras.nu) kan je een mooie sangakuposter (zie bijlage) aankopen.

In bijlage zit ook nog het inspirerende eindwerk van een leerlinge van Hemelsdaele (Brugge) (toegevoegd in 2015).

Bijlagen:
De Wilde An-Sofie Eindwerk Wiskunde 2015 - Sangaku.docx (2.6 MB)   
sangakuposter.pdf (159.6 KB)   
SANGAKU_bewijs.pdf (70 KB)