|
Een van de meest intrigerende curven is de cycloïde die ontstaat wanneer men de baan volgt van een punt op een cirkelvormig wiel dat op een vlak terrein rolt zonder glijden.
De animatie hieronder toont hoe een cycloïde (rode curve) ontstaat.
Cycloïde en principe van Mamikon - GeoGebra Dynamisch werkblad
Wiskundigen stelden zich de vraag hoeveel de oppervlakte bedraagt onder één cycloïdeboog.
Men kan die uiteraard via de klassieke integraalrekening bepalen (zie bijlage).
Het is verbazingwekkend dat die oppervlakte precies gelijk is aan de drie keer de oppervlakte van de rollende cirkel (zie onderstaande figuur).

Er bestaat echter een andere en heel verrassende manier om de oppervlakte onder één cycloïdeboog te berekenen.
Die methode werd ontdekt door de Armeense student Mamikon Mnatsakanian in 1959.
Zijn professoren geloofden niet in zijn vondst en pas in 1981 kreeg Mamikon de erkenning voor zijn mooie vondst.
Hij bewees toen het volgende resultaat:
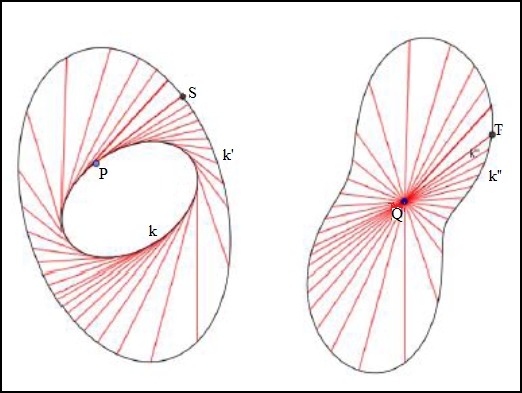
Om de oppervlakte tussen twee krommen
k en k' te bepalen, neem je een willekeurig punt P op de kromme k.
Teken in P de raaklijn aan k die de kromme k' snijdt in S (linkse figuur
hieronder).
Neem nu een vast punt Q en verschuif het lijnstuk [PS] naar [QT].
Als P de kromme k doorloopt zal het punt T de kromme k" doorlopen (rechtse
figuur hieronder).
Dan is de oppervlakte tussen k en k' gelijk aan de oppervlakte binnen de kromme
k".
We passen dit principe toe voor de berekening van de oppervlakte onder één cycloïdeboog.
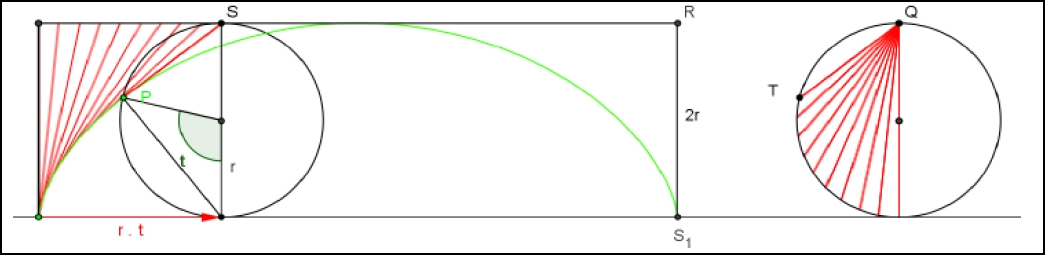
Oppervlakte van de rechthoek (links) = (2πr)(2r) = 4πr2.
Oppervlakte tussen de cycloïde en de rechthoek = oppervlakte cirkel (rechts) = πr2 .
Bijgevolg is de oppervlakte onder één cycloïdeboog = 3πr2 .
Meer informatie hierover lees je in de bijlagen.
Met dank aan collega's Riggy Van de Wiele en Jef De Langhe die me op de voorbije dag van de wiskunde (19 november 2011) hierop attent maakten.
Bijlagen:
A visual vpproach to calculus and Mamikon's principle.pdf (779.4 KB)
Het principe van Mamikon.pdf (276.8 KB)
13-01-2012 om 00:00
geschreven door Luc Gheysens 
|
