Heel wat studenten zijn ervan overtuigd dat een functie constant is in een interval als de eerste afgeleide van die functie nul is in alle punten van dit interval.

Het nul-zijn van de eerste afgeleide is wel een nodige voorwaarde opdat een functie constant zou zijn, maar die voorwaarde is niet voldoende!

Voorbeeld. f : IR → IR : x → f(x) = arctan (x) + arctan (1/x).
Men rekent gemakkelijk na dat de eerste afgeleide van deze functie nul is:
f '(x) = 1/(1 + x²) + (-1/x²)/(1 + 1/x²) = 1/(1 + x²)  –  1/(1 + x²) = 0.
Wanneer we echter de grafiek van deze functie bekijken, blijkt dat voor alle strikt negatieve x-waarden f(x) = -π/2 en voor alle strikt positieve x-waarden is f(x) = π/2.

We kunnen dit ook schrijven als f(x) = (π/2) . sign(x) omdat de sign-functie gedefineerd is door: sign(x) = 1 voor x > 0 en sign(x) = -1 voor x < 0.

Hieronder zie je hoe je dit eenvoudig met een grafische rekenmachine kunt verifiëren.

 Een continue functie is constant in een interval als en slechts als de eerste afgeleide van die functie nul is in alle punten van dit interval!
Immers, om te bewijzen dat uit het feit dat f '(x) = 0 voor alle x-waarden in [a,b] volgt dat f constant is in [a,b]
steunt men op de stelling van Lagrange en hiervoor is de voorwaarde van continu-zijn nodig.

Opgave.
Bepaal de eerste afgeleide van beide onderstaande functies. Teken de grafiek. Zijn dit constante functies?
1) g : IR → IR : x → f(x) = arctan (2x + 1) + arctan (1 + 1/x).
2) h : IR → IR : x → f(x) = arctan ((1 – x)/(1 + x)) + arctan (x).

Oplossing.
1) g(x) = (π/2) . sign(x) + π/4.
2) h(x) =(π/2) . sign(x + 1) – π/4. 

Blijf verwonderd!

08-07-2010 om 00:00 geschreven door Luc Gheysens  

Teken n²  cirkels in een vierkant met zijde a, zodat er n rijen van n cirkels zijn die elkaar twee aan twee uitwendig raken

en zodat de cirkels bovendien raken aan de zijden van het vierkant.

Op de onderstaande figuur werden zo respectievelijk 3² = 9 en 4² = 16 cirkels getekend en de cirkelschijven werden ingekleurd.

Toon aan dat er op beide figuren evenveel witruimte overblijft binnen het vierkant.

Dit blijkt bovendien onafhankelijk te zijn van het gekozen  getal n. 

   

Oplossing.

De straal van elk van de n² cirkels is gelijk aan a/(2n) en bijgevolg is de totale oppervlakte van de n² cirkels gelijk aan n². πa²/(4n²) = πa²/4.

De oppervlakte van de witruimte is dan gelijk aan (1 – π/4)a²

(dit is precies het verschil van de oppervlakte van het vierkant met zijde a en de oppervlakte van de ingeschreven cirkel in dit vierkant) en hangt dus niet af van n.

Toon aan dat deze eigenschap ook geldig is voor n³ bollen die in een kubus met ribbe a worden geplaatst.

08-07-2010 om 00:00 geschreven door Luc Gheysens  

Abu Ja'far Muhammed ibn Musa al-Chwarizmi werd rond 780 in Bagdad geboren.
De naam al-Chwarizmi betekent letterlijk "afkomstig uit Chwarizmi", een streek in het huidige Oezbekistan. 
Het belang van zijn wetenschappelijk werk blijkt o.a. uit het feit dat het woord algoritme aan zijn naam ontleend is.
Hij leverde grote bijdragen aan gebieden als algebra, trigonometrie, astronomie en astrologie, geografie en cartografie.
Zijn systematische en logische aanpak van het oplossen van lineaire en kwadratische vergelijkingen gaven gestalte aan de algebra,
 een vakgebied dat zijn naam ontleent aan Chwarizmi's beroemde boek over het vakgebied: Hisab al-jabr wa al-muqabala,
"de theorie van transformatie en herstel", refererend aan de manieren waarop deeltermen in algebraïsche termen gemanipuleerd kunnen worden.

Bron: wikipedia.

We geven hieronder een voorbeeld waaruit blijkt op welke ingenieuze manier al-Chwarizmi
erin slaagde een oplossing te vinden van enkele eenvoudige tweedegraadsvergelijkingen. 

Uiteraard had hij geen echte algebra te beschikking en moest hij zich - in de Griekse traditie -
behelpen met meetkundige figuren en de oppervlakte ervan.

We illustreren zijn methode aan de hand van de vergelijking x² + 10x = 39. 

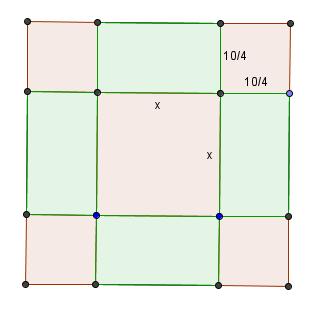
Hij vertrekt van een vierkant met zijde x en dus met oppervlakte x².
Hij vult deze figuur daarna aan met vier rechthoeken waarvan één zijde lengte x heeft en de andere zijde lengte 10/4.
Die vier rechthoeken samen hebben dan een oppervlakte 10x.
De vraag is nu hoe hij de afmeting x moet kiezen zodat de vijf vierhoeken (het vierkant en de vier rechthoeken)
samen een oppervlakte hebben die gelijk is aan 39.
Hij vervolledigt hiervoor de figuur door aan de vier hoeken een vierkantje te tekenen met zijde 10/4.

De oppervlakte van deze vier vierkantjes samen is gelijk aan 25
en bijgevolg moet de oppervlakte van het groot vierkant (de gehele figuur) gelijk zijn aan 39 + 25 = 64.
Maar dan kan hij hieruit direct besluiten dat de zijde van het grote vierkant lengte 8 heeft. 

Bijgevolg is x = 8 – 2 . (10/4) = 8 – 5 = 3.

 OPGAVE. Pas de methode van al-Chwarizmi toe om een oplossing te bepalen van de vergelijking x² + 3x/2 = 10.

Lukt dit?

07-07-2010 om 00:00 geschreven door Luc Gheysens  

Een rotatie of draaiing om een punt over een bepaalde hoek is een eenvoudige transformatie

waarmee men in de vlakke meetkunde ogenschijnlijk moeilijk bewijsbare eigenschappen 'in een handomdraai' bewezen krijgt.

Een mooi voorbeeld hiervan staat hieronder afgebeeld (met dank aan collega Eddy Jennekens).

Wanneer men op twee zijden van een willekeurige driehoek ABC buitenwaarts vierkanten construeert (op de figuur de vierkanten ADEC en ABFG), 

dan zijn de lijnstukken [DB] en [CG] even lang en bovendien staat ze loodrecht op elkaar.

Voor het bewijs volstaat het op het lijnstuk [DB] een draaiing toe te passen rond het punt A over een hoek van -90°. 

GESNAPT?

06-07-2010 om 00:00 geschreven door Luc Gheysens  

DE RECHTE VAN SIMSON

Op het voorbije congres van de Vlaamse Vereniging voor Wiskundeleraren (www.vvwl.be) op 1 en 2 juli 2010 in Blankenberge

maakte collega Eddy Jennekens me attent op een 'vergeten' stelling uit de vlakke meetkunde.

Wanneer men een willekeurig punt P op de omgeschreven cirkel van een willekeurige driehoek ABC

loodrecht projecteert op de drie zijden (zijlijnen) van deze driehoek, dan zijn de drie projectiepunten collineair.

De rechte door de projectiepunten R, S en T is de rechte van Simson, genoemd naar de Britse wiskundige Robert Simson (1687-1768).

Bijlagen:
Rechte van Simson.doc (172.5 KB)   

Op Youtube circuleren heel wat filmpjes waarin een wiskundige truc met kaarten wordt getoond (en soms ook wordt uitgelegd).

De 'Card Trick Teacher' is hierbij mijn favoriet. 

http://www.thecardtrickteacher.com/

Graag één truc (die voldoende concentratie vergt) bij wijze van voorbeeld.

05-07-2010 om 00:00 geschreven door Luc Gheysens