|
Gran elefant dret, Miquel Barceló, 2009.
Tijdens een tussenstop in Avignon begin augustus 2010 botsten we op een intrigerend kunstwerk van Miquel Barceló,
dat ter gelegenheid van de speciale tentoonstelling Terra-Mare van het werk van deze kunstenaar was ontleend
uit de Galerie Bruno Bischlofberger in Zürich en opgesteld stond op het plein voor het Palais des Papes.
Ondanks het feit dat heel wat toeristen even tegen deze reusachtige olifant kwamen leunen,
bleef hij onwrikbaar in evenwicht staan.
Het herinnerde me er aan dat als een lichaam een steunvlak heeft, het niet zal omvallen zolang de loodlijn uit het zwaartepunt dit vlak snijdt.
Bij een driehoek is het zwaartepunt het snijpunt van de drie zwaartelijnen.
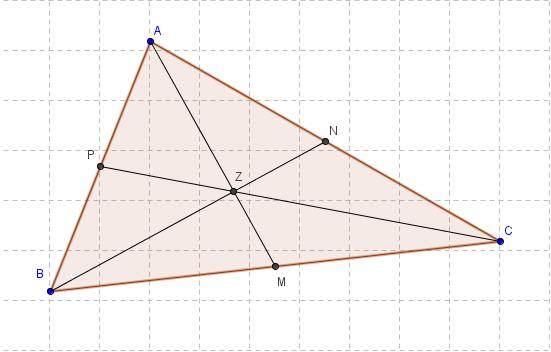
Op de onderstaande figuur is het zwaartepunt Z van driehoek ΔABC getekend.
Men kan gemakkelijk aantonen (hoe doe je dat?) dat de drie driehoeken ΔZAB, ΔZBC en ΔZCA dezelfde oppervlakte hebben
en meteen kan je ook aantonen dat er zes even grote driehoeken op deze figuur staan, nl. ΔZAP, ΔZPB, ΔZBM, ΔZMC, ΔZCN en ΔZNA.
Tip. Waarom is de afstand van Z tot de zijde [BC] van de driehoek gelijk aan één derde van de hoogte uit A?
Het zwaartepunt van een vlakke figuur is dus het punt waaronder je een speld kunt plaatsen
waarop de figuur dan in evenwicht zou kunnen blijven staan.
Bij een cirkelschijf is het middelpunt uiteraard het zwaartepunt.
Maar weet je ook waar het zwaartepunt van een halve cirkelschijf ligt?
Dit probleem kan je oplossen met behulp van bepaalde integralen.
In bijlage vind je een powerpointpresentatie waarin de algemene formules voor de berekening van de coördinaten (Zx, Zy)
van het zwaartepunt Z van een vlakke figuur terug te vinden zijn.
Probeer hiermee eens aan te tonen dat het zwaartepunt Z van een halve cirkelschijf
(neem als vergelijking van de cirkel y = √(r² - x ²)) als coördinaten Zx = 0 en Zy = (4r)/(3π) heeft.
Door gebruik te maken van de zogenaamde stelling van Pappus kan je dit resultaat vrij direct verifiëren.
Stelling van Pappus
Als een vlakke figuur F wentelt rond een as die in hetzelfde vlak ligt en de vlakke figuur F niet snijdt,
dan is de inhoud van het ontstane omwentelingslichaam gelijk
aan het product van de oppervlakte van F en de omtrek van de cirkel beschreven door het zwaartepunt Z van F.
Hoe vind je hiermee de bovenstaande formules terug voor het zwaartepunt van een halve cirkelschijf ?
 In bijlage vind je nog een uitdagende werkopdracht over het zwaartepunt van vlakke en van 3D-figuren.
Bron: http://schoolweb1.rago.be Bijlagen:
Toepassing bepaalde integraal.pps (779.5 KB)
Werktekst over het zwaartepunt.pdf (45.3 KB)
23-08-2010 om 00:00
geschreven door Luc Gheysens 
|
