|

Srinivasa Ramanujan (1887-1920)
. Weinig wiskundigen spreken zo zeer tot de verbeelding als de Indiër Ramanujan.
Deze autodidact volgende eigenlijk
nooit wiskundeles en studeerde tijdens zijn korte leven wiskunde uit boeken
en volledig geïsoleerd van de wiskundewereld van zijn tijd.
Hij gaf dan ook op het einde van zijn korte leven (hij stierf aan tuberculose
voor hij 33 jaar werd) toe
dat hij heel veel tijd had verloren door alles zelf te willen uitpluizen.
Ramanujan wordt soms 'de formulemaker' genoemd.
Hij slaagde er immers in op eigen houtje een aantal merkwaardige formules op te
stellen
waarmee hij wiskundeprofessoren wist te verbazen.
Eén van zijn bekendste formules is de
somformule die een benadering voor het getal pi oplevert:

Als je namelijk enkel de eerste term uit deze som neemt, bekomt je een benadering voor pi die al tot op 6 decimalen juist is:
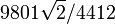
wat gelijk is aan 3,1415927...
In 1913 stuurde hij brieven
naar verschillende Engels universiteiten
en het was Prof. G. H. Hardy uit Cambridge die direct in de talenten van
Ramanujan geloofde.
Hij haalde hem dan ook naar Cambridge om met hem samen te werken
Het volgende verhaaltje toont aan welk uitzonderlijk talent voor getallen Ramanujan wel had.
Toen Prof. Hardy hem ging bezoeken in het ziekenhuis van Putney, vertelde hij hem dat hij naar het ziekenhuis was gekomen met een taxi die het nummer 1729 had.
"Dat is heel interessant", zei de zieke Ramanujan, "het is immers het kleinste getal dat op twee verschillende manieren te schrijven is als een som van twee derdemachten, nl. 1729 = 1³ + 12³ en 1729 = 9³ + 10³." Sedertdien spreken wiskundigen over taxicab numbers. Meer hierover lees je op http://mathworld.wolfram.com/TaxicabNumber.html.
Zelf heb ik me altijd een beetje verbaasd over kwadraten en derdemachten en verbanden ertussen. Het volgende leuke resultaat mag hier dan ook niet ontbreken:
Neem twee natuurlijke getallen. Kwadrateer ze en tel de kwadraten bij elkaar op. Neem hiervan de derdemacht. Het bekomen getal is zelf weer te schrijven als de som van twee kwadraten.
Enkele voorbeelden.
a = 1 en b = 2 : (12 + 22)3 = 53 = 125 en 125 = 22 + 112.
a = 2 en b = 3 : (22 + 32)3 = 133 = 2197 en 2197 = 92 + 462.
Voor het algemeen bewijs hiervan (in bijlage) gebruikte ik complexe getallen.
Collega Els Coussement, docente wiskunde aan de Arteveldehogeschool in Gent (Campus Kattenberg) bezorgde me een alternatief en eenvoudig bewijs van deze eigenschap.
Merkwaardig genoeg toont ze hiermee aan dat de som van de twee kwadraten niet uniek is. Ziehier het bewijs:
(a2 + b2)3 = (a2 + b2) (a2 + b2)2 = a2 (a2 + b2)2 + b2 (a2 + b2)2 = [a(a2 + b2)]2 + [b(a2 + b2)]2.
Hiermee vinden we dan voor
a = 1 en b = 2 : 125 = 52 + 102
a = 2 en b = 3 : 2197 = 262 + 392.
    Bijlagen:
Kwadraten en derdemachten.pdf (51.1 KB)
30-01-2012 om 00:00
geschreven door Luc Gheysens 
|
