MAGISCH PRIEMVIERKANT

In zijn boek 'Madachy's Mathematical recreations'
vermeldt J.S. Madachy enkele merkwaardige magische priemvierkanten.
Dit zijn magische vierkanten waarbij alle getallen priemgetallen zijn.

Dit magisch vierkant is het priemvierkant met de kleinst mogelijke magische constante
(som van de 3 getallen in elke rij, elke kolom en op de twee diagonalen), nl. 177.
Het staat op naam van Rudolf Ondrejka (1929-2001)
die blijkbaar geobsedeerd was van merkwaardige priemgetallen (zie bijlage).

******************************************************************************************************

De stelling van Green-Tao, in 2004 bewezen door Ben Green en Terence Tao
toont aan dat de ordening van priemgetallen willekeurig lange rekenkundige rijen bevat.
Met andere woorden voor elk natuurlijk getal k bestaan er​ rekenkundige rijen van priemgetallen van lengte k.

Zo staan er bijvoorbeeld in het volgende rijtje negen priemgetallen
waarbij het verschil tussen elke twee opeenvolgende getallen gelijk is aan 210:

199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879.

DENKOEFENING MET DEZE RIJ PRIEMGETALLEN

Vervang in dit Lo-Shu-magisch vierkant
het cijfer 1 door 199, het cijfer 2 door 409, het cijfer 3 door 619 ... enzovoort
tot en met het cijfer 9 door 1879. 
Meteen bekom je een magisch priemvierkant.



 Kan je ook verklaren waarom dit dan een magisch vierkant is?

Bijlagen:
Top 10 van de priemgetallen - R. Ondrejka.pdf (219 KB)   

WAAROM WISKUNDE STUDEREN?

De TED-conferenties (Technology, Entertainment, Design) werden in 1984 voor het eerst georganiseerd in Californië.
Tijdens deze jaarlijkse vierdaagse bijeenkomst worden sprekers uitgenodigd
 om in maximaal 18 minuten "de presentatie van hun leven" te geven
over hun gebied van expertise, over een bepaald project,
of iets waarvan zij vinden dat het een idee is dat verspreid moet worden.

Alhoewel iedereen het nut van wiskunde kent vanuit berekeningen en concrete toepassingen,
 wijst Arthur Benjamin er ons in de onderstaande video op dat wiskunde ook uitnodigt om creatief te denken. 
In 6 minuten laat hij ons op een enthousiaste en aanstekekelijke manier
meegenieten van de zuivere schoonheid van de wiskunde via de magie van de Fibonaccigetallen.

Ik verwijs in dit verband graag naar een eerdere publicatie op mijn blog:
Fibonacci in het kwadraat (06-11-2013).

18-01-2014 om 00:00 geschreven door Luc Gheysens  

17-01-2014 om 11:35 geschreven door Luc Gheysens  

DE DETERMINANTFORMULE
VOOR DE OPPERVLAKTE VAN EEN DRIEHOEK 

Van een gegeven driehoek ABC met co(A) = (x₁, y₁), co(B) = (x₂, y₂) en co(C) = (x₃, y₃)
is de oppervlakte gelijk aan

Het bewijs hiervan zit in de bijlage

Hierbij moet men de absolute waarde nemen van een determinant van orde 3.
Die is eenvoudig te herleiden tot 3 determinanten van orde 2.
Als men bovendien de hoekpunten van de driehoek in een volgorde plaatst
zodat men de omtrek vanaf  A via B naar C in tegenwijzerzin loopt (zie onderstaande figuur),
hoeft men ook de absolute waarde niet meer te nemen.

In het volgende (Engelstalig) filmpje zie je hoe men zo
de oppervlakte van de bovenstaande driehoek berekent.

Bijlagen:
Determinantformule oppervlakte driehoek.pdf (114.8 KB)   

 

PROBLEEM 18

Twee cirkels C₁ en C₂ met middelpunten M en N en stralen r₁ en r₂ raken elkaar uitwendig in het punt P.
[AB] en [CD] zijn twee evenwijdige middellijnen van deze cirkels.
Een derde cirkel C₃ met middelpunt O gaat door de punten A, B, C en D.
Toon aan dat de gebieden die in het rood en het groen gekleurd zijn
(zie onderstaande figuur) dezelfde oppervlakte hebben.

UITVINDING 18

Bijlagen:
COSMOSPROBLEEM 18_oplossing.pdf (205.3 KB)   

REGELMAAT VERSUS BEWIJS

Bij de studie van rijen is een klassieke vraag:
zoek de volgende term in de rij.

Enkel voorbeelden:
1, 3, 9, 27, ...    (volgende term: 81)
1, 2, 4, 7, 11, ...  (volgende term: 16)
1, 4, 13, 40, 121, ... (volgende term: 364 want telkens maal 3 plus 1)
3, 1, 4, 1, 5, ... (volgende term: 9 want π = 3,14159...)

Bij het onderstaande probleem komt men echter tot een 'verrassende' volgende term.



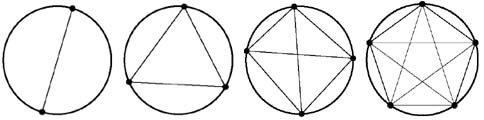
Neem 2, 3, 4, 5, ... punten op een cirkelomtrek
en verbind elk punt met alle andere punten.
Wat is dan het maximale aantal gebieden waarin de cirkelschijf wordt verdeeld
en hoeveel gebieden krijg je maximaal wanneer je 6 punten kiest?

Op de bovenstaande figuur lees je het antwoord af
voor 2 punten → 2 gebieden
voor 3 punten → 4 gebieden
voor 4 punten → 8 gebieden
voor 5 punten → 16 gebieden
en dus voor 6 punten → ??? gebieden.
Logischerwijze denk je dan aan 32 gebieden, maar dit blijkt niet juist te zijn.



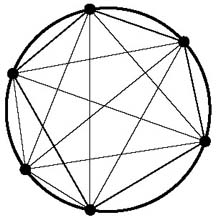
Tel je dit zelf even na?

En hier zit precies de kracht van een wiskundig bewijs!
Leo Moser bewees de algemene formule voor het aantal gebieden bij n punten:



of met behulp van binomiaalcoëfficiënten:

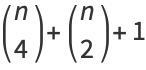
Het volstaat dus niet vast te stellen dat een bewering waar is
in een groot aantal gevallen waarvoor men die verifieert.
Het onderstaande filmpje maakt dit nog eens duidelijk.

Bijlagen:
Regions in a circle.pdf (48.9 KB)   

PARADOX VAN BERTRAND



Joseph Bertrand
Calcul des probabilités (1889)
 
Wanneer men in de kansberekening te maken heeft men kansen
waarbij er een oneindig aantal keuzes mogelijk zijn
(bijvoorbeeld bij het kiezen van een punt in een driehoek of in een cirkel)
dan kan men tot schijnbaar tegenstrijdige resultaten komen.

Het typevoorbeeld hiervan is de paradox van Bertrand.
Bron: http://www.hhofstede.nl/paradoxen/bertrand.htm .

Teken een cirkel en teken daarin een willekeurige koorde.
        Hoe groot is dan de kans dat deze koorde langer is
dan de zijde van de ingeschreven gelijkzijdige driehoek? 

Er blijken hier drie verschillende manieren te zijn om die kans te berekenen.    

METHODE 1
Draai de driehoek zodat de (groene) koorde evenwijdig is met één van de zijden.
Het midden van de koorde ligt dan op de (blauwe) middelloodlijn van die zijde.
De gekozen koorde is langer dan de zijde van de driehoek
als het midden van die koorde tussen de twee rode punten ligt. 
Dus is de kans = 1/2.      

METHODE 2
Draai de driehoek zodat een hoekpunt ervan samenvalt met een (rood) eindpunt van de (groene) koorde.
Elke koorde maakt een hoek met de raaklijn in dat (rood) punt die varieert van 0° tot 180°.
De gekozen koorde is langer dan de zijde van de driehoek
als ze binnen de tophoek van de driehoek valt.
Die tophoek is 60° en bijgevolg is de kans 1/3.



METHODE 3
Teken de ingeschreven cirkel C_i van de gelijkzijdige driehoek.
De straal van deze cirkel is de helft van de straal van de omgeschreven cirkel C_O
en dus is de oppervlakte van C_i gelijk aan 1/4 van de oppervlakte van C_O.
De gekozen (groene) koorde is langer dan de zijde van de driehoek
als het midden van die koorde binnen C_i valt
en bijgevolg is die kans 1/4.

           Bij dit soort van problemen moet men dus nader omschrijven hoe dat lukraak kiezen gebeurt!

14-01-2014 om 00:00 geschreven door Luc Gheysens  

WISKUNDE EN LANDMEETKUNDE

Prof. Dr. Ir. Alain De Wulf, een oud-leerling die al jarenlang verbonden is aan de afdeling Landmeetkunde (UGent) 
bezorgde me een reeks uitdagende opgaven die je met behulp van driehoeksmeting en vlakke meetkunde kunt oplossen.

Benieuwd hoeveel laatstejaarsstudenten van het middelbaar onderwijs deze twee opgaven zouden kunnen oplossen.

Bijlagen:
Opgaven landmeetkunde - oplossingen.pdf (233.8 KB)