Straks nemen weer heel wat jongeren deel
aan het toelatingsexamen voor de Koninklijke Militaire School.

Op http://www.rma.ac.be/nl/index.html vind je alle informatie.

In bijlage hebben we een aantal inspirerende vragen verzameld
voor het toelatingsexamen wiskunde.
In de vragenreeks viel mijn oog op deze opgave:

Bepaal twee positieve reële getallen waarvan
de som gelijk is aan het product en aan het verschil van de kwadraten.

Het kleinste getal blijkt dan gelijk te zijn aan het getal van de gulden snede:

 
Voor de Faculteit Polytechnische is er een aparte
en heel wat moeilijkere reeks vragen.
Daar vonden we onze inspiratie voor deze leuke oneigenlijke integraal
die een verband legt tussen 0, 1, 2, 4, e (het getal van Euler), ∞ en π.
Je kan de integraal berekenen via de substitutie t = e^x/4.

Bijlagen:
Toelatingsexamen KMS - Faculteit Polytechnische.pdf (380.1 KB)   
Toelatingsexamen KMS - wiskundevragen.pdf (1.4 MB)   

DE VIER-KWADRATEN-STELLING

In 1770 bewees de Italiaanse wiskundige Joseph-Louis Lagrange
(die vaak als een Fransman wordt aanzien omdat hij geruimde tijd in Parijs doceerde)
een merkwaardige stelling:

"Elk natuurlijk getal kan geschreven worden als de som van vier kwadraten."

Merk op: in veel gevallen is deze schrijfwijze niet uniek
en ook moet men soms 0² toelaten als één van de vier termen van de som.

Zo is bijvoorbeeld
49 = 1² + 4² + 4² + 4²
   = 0² + 2² +3² + 6²
    = 2² + 2² + 4² + 5²
    = 0² + 0² + 0² + 7².

De Griekse wiskundigen interpreteerden kwadraten als vierkanten
en bijgevolg zouden ze op zoek zijn gegaan naar een meetkundige voorstelling.
Hieronder zie je een 'Griekse' oplossing (dissectie in 5 stukken) waaruit blijkt dat 7² = 2² + 3² + 6².

Op http://www.alpertron.com.ar/FSQUARES.HTM
staat een applet dat een willekeurig getal
schrijft als de som van vier kwadraten
(0² moet je er soms zelf bij denken).

Op 10 april 2013 is het precies 200 jaar geleden dat Lagrange is overleden.
Als eerbetoon werd hij begraven in het Panthéon in Parijs
en is zijn naam één van de 72 namen van eminente Franse wetenschappers
die gegraveerd staan op de Eiffeltoren.
Zie http://nl.wikipedia.org/wiki/72_namen_op_de_Eiffeltoren .

Fiat lux!

07-04-2013 om 00:00 geschreven door Luc Gheysens  

Straks nemen weer heel wat jongeren deel
aan het toelatingsexamen voor de Koninklijke Militaire School.

Op http://www.rma.ac.be/nl/index.html vind je alle informatie.

In bijlage hebben we een aantal inspirerende vragen verzameld
voor het toelatingsexamen wiskunde.
In de vragenreeks viel mijn oog op deze opgave:

Bepaal twee positieve reële getallen waarvan
de som gelijk is aan het product en aan het verschil van de kwadraten.

Het kleinste getal blijkt dan gelijk te zijn aan het getal van de gulden snede:

 
Voor de Faculteit Polytechnische is er een aparte
en heel wat moeilijkere reeks vragen.
Daar vonden we onze inspiratie voor deze leuke oneigenlijke integraal
die een verband legt tussen 0, 1, 2, 4, e (het getal van Euler), ∞ en π.
Je kunt de integraal berekenen via de substitutie t = e^x/4 :

Bijlagen:
Toelatingsexamen KMS - Faculteit Polytechnische.pdf (380.1 KB)   
Toelatingsexamen KMS - wiskundevragen.pdf (1.4 MB)   

MERKWAARDIGE CIRKELS

Als de grootste cirkel op deze figuur een straal van 6 cm heeft,
hoe groot is dan de straal van de groene, gele en blauwe cirkels?

Antwoord: 3 cm, 2 cm en 1 cm.
Dit is een leuke oefening op de stelling van Pythagoras.

Voor een uitgeschreven oplossing
en nog veel meer mooie opgaven
verwijzen we naar http://mathafou.free.fr/ .

07-04-2013 om 00:00 geschreven door Luc Gheysens  

HEURIST is een woord dat blijkbaar niet in 
Van Dale's Groot woordenboek van de Nederlandse taal is opgenomen.

Nochtans zou elke wiskundeleraar een HEURIST moeten zijn
die zijn leerlingen allerlei HEURISTIEKEN (zie bijlage) aanleert.

Zelf zou ik een HEURIST definiëren als iemand die
(bijna dagelijks) bezig is met probleemoplossend denken
 en op een creatieve manier allerlei oplossingsstrategieën toepast.

HEURIST is ook een zeven-letterwoord dat verwijst naar
HUMOR, waarmee je jouw lessen kruidt
EXPERTISE, wat elke leerling op de eerste plaats van de leraar verwacht
UITDAGING, waarmee je jouw leerlingen prikkelt
REFLECTIE, bij foutenanalyse en controle van een resultaat
INTERACTIE, via variatie in werkvormen (doceren, groepswerk, ICT...)
SUCCESERVARING, het allerbelangrijkste voor de leerling (en de leraar)
TOEPASSINGEN en Theorie, een gezond evenwicht!

In de figuur zit een mooie stelling verborgen
die in de literatuur bekend staat als
de stelling van de zeven cirkels (1974).

Kan je zelf ontdekken wat die stelling uit de vlakke meetkunde beweert?
Info op http://mathworld.wolfram.com/SevenCirclesTheorem.html .

Bijlagen:
HEURISTIEKEN.pdf (63.5 KB)   

DE KWADRATUUR VAN HET KLAVERTJE VIER



Is het mogelijk een vierkant te construeren
dat dezelfde oppervlakte heeft als de gekleurde figuur hierboven
die is opgebouwd met vier even grote cirkels die door eenzelfde punt gaan
(het witte gedeelte niet meegerekend)?

Als de vier cirkels een straal r hebben
dan is de gekleurde oppervlakte gelijk aan
4πr²  –  16(πr²/4  – r²/2) = 8r².
Dit is gelijk aan de oppervlakte van een vierkant met zijden 2√2 r.

En ja hoor, de kwadratuur lukt perfect zoals uit de twee onderstaande figuren blijkt!

        

05-04-2013 om 00:00 geschreven door Luc Gheysens  

CIRKELPROBLEEM

Een verrassend eenvoudig bewijs vind je in de bijlage.
Graag zelf eerst even zoeken a.u.b.

Bijlagen:
Cirkelprobleem opgelost.pdf (140.3 KB)   

De Amerikaanse amateurwiskundige Sam Loyd (1841-1911)
bedacht een aantal schitterende puzzels
die hij telkens in een verhaaltje wist in te kleden.

Deze Guido-mozaïek-puzzel bestaat er in een vierkant van 5 x 5 vakjes
in zo weinig mogelijk stukken te verdelen
waarmee je dan een vierkant van 4 x 4 vakjes
en een vierkant van 3 x 3 vakjes kunt vormen.

Dit is in feite een mooie variatie op de stelling van Pythagoras
die garandeert dat 3² + 4² = 5².

Met GeoGebra hebben we de onderstaande oplossing uitgetekend.



De puzzels van Sam Loyd vind je op www.samloyd.com 

03-04-2013 om 00:00 geschreven door Luc Gheysens  

HOOGTEPUNT DEEL 2

Teken eens een driehoek ABC waarvan de drie hoekpunten op de eenheidscirkel liggen
(de cirkel met de oorsprong als middelpunt en met een straal gelijk aan 1).
Als de hoekpunten van de driehoek de volgende coördinaten hebben
A(x₁, y₁), B(x₂, y₂) en C(x₃, y₃)
dan is de coördinaat van het hoogtepunt H van driehoek ABC
bepaald door H(x₁ + x₂ + x₃, y₁ + y₂ + y₃).

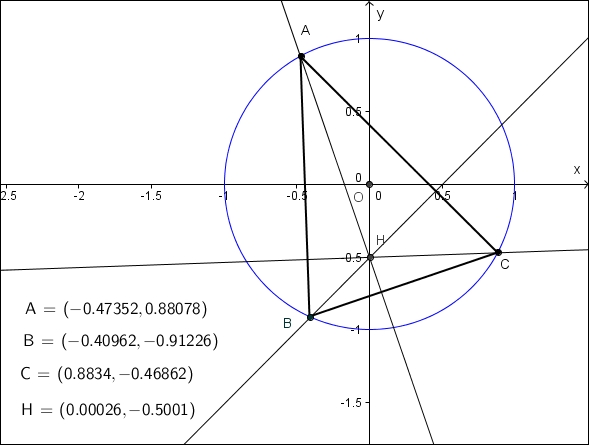
Hieronder staat een voorbeeld ter illustratie (getekend met GeoGebra).

Je kunt het rekenwerk gemakkelijk controleren aangezien H nagenoeg (0, - 0,5) als coördinaat heeft.

Een bewijs zit in bijlage.

Bijlagen:
Hoogtepunt driehoek en eenheidscirkel.pdf (201.8 KB)   

VIERKANTSWORTELS EN VWO

 © 2008 Peter Grabarchuk. All Rights Reserved.

Peter Grabarchuk is de auteur van deze eenvoudige (?) puzzel met vierkantswortels.
De som van de getallen op twee van de vier puzzelstukjes is gelijk. 
Kan jij ontdekken over welke twee puzzelstukjes het hier gaat? 

Meer puzzels van Peter Grabarchuk op PeterPuzzle.com

En ook op de voorbije Vlaamse Wiskunde Olympiade
doken twee meerkeuzevragen op over vierkantswortels.
(die niet zo goed werden beantwoord!)

Vind jij de juiste antwoorden?

02-04-2013 om 00:00 geschreven door Luc Gheysens