|
NUM'ART is een artistiek project bedacht door Luc Janus.
Hij zet hierbij elke week een getal op een artistieke manier in de kijker.
*********************************************************************************************************
91

Taxi - Luc Janus
*********************************************************************************************************************
Aan het feit dat 91 = 63 53 = 33 + 43 is een merkwaardig wiskundig verhaal verbonden.
TAXICAB-GETALLEN EN CABTAXI-GETALLEN
Het n-de taxicab-getal Ta(n) is het kleinste natuurlijk getal dat op n verschillende manieren kan geschreven
worden als de som van twee positieve derdemachten.
De herkomst van de naam "taxicab-getal" gaat terug op een anecdote
over de Indiase wiskundige Ramanujan verteld door Godfrey Harold Hardy.
Hardy was met taxi nummer 1729 naar het ziekbed van Ramanujan gekomen.
Hij zei tegen Ramanujan dat hij dit maar een saai getal vond.
Maar Ramanujan vond van niet, want, zei hij,
"het is het kleinste getal dat op twee verschillende manieren
als de som van twee positieve derdemachten kan worden uitgedrukt".
Inderdaad: 1729 = 13 + 123 = 93 + 103.
En dit zijn de eerste drie taxicab-getallen:
-
-
 . -
-
Naar analogie hiermee hebben wiskundigen dan ook cab-taxigetallen gedefinieerd.
-
-
Het n-de cabtaxi-getal is het kleinste natuurlijk getal dat op n verschillende manieren kan geschreven
worden als de som van twee (niet noodzakelijk positieve) derdemachten.
-
-
Dit zijn de eerste drie cabtaxi-getallen:
1 = 13 + 03
91 = 63 53 = 33 + 43
728 = 123 103 = 93 13 = 63 + 83
*********************************************************************************************************************
In de tafel van 91 vormen de cijfers van 1 tot en met 9 een merkwaardig patroon.

Bron: RETOS MATEMÁTICOS
*********************************************************************************************************************
Wat is het volgende nummer is deze rij?
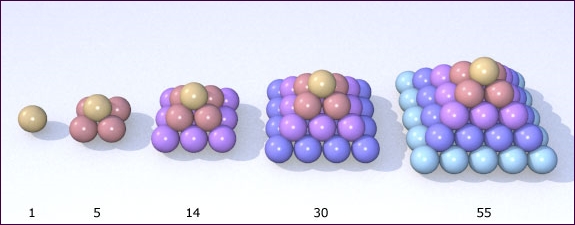
Antwoord: 91 = 12 + 22 + 32 + 42 + 52 + 62 is het zesde vierkant piramidegetal.
*********************************************************************************************************************
Wat is het 13de getal uit deze rij?
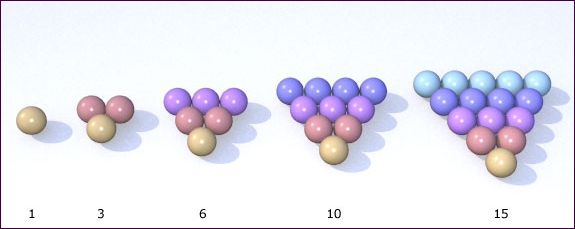
Antwoord: 91 = 1 + 2 + 3 + ... + 13 is het 13de driehoeksgetal.
*********************************************************************************************************************
Wat is het volgende getal in deze rij?
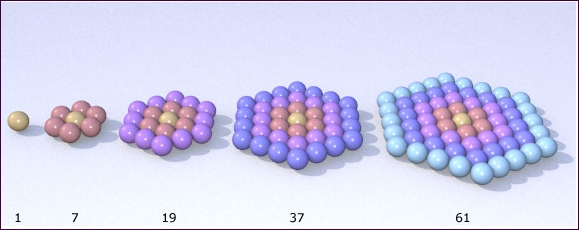
Antwoord: 91 = 1 + 6 + 12 + 18 + 24 + 30 is het zesde gecentreerd zeshoeksgetal.
Deze getallen vindt men via de recursieformule t(n) = t(n 1) + 6(n 1) of via het expliciete voorschrift t(n) = 3n(n 1) + 1.
*********************************************************************************************************************
91 = 92 + 91 + 90
91 = 12 + 42 + 52 + 72
91 = 12 + 32 + 92
91 = 462 452

04-04-2016 om 00:00
geschreven door Luc Gheysens 
|
