WISKUNDE BIJ DE GOUDSMID

Een goudsmid heeft een ketting gemaakt die bestaat uit 
18 karaat gouden ringetjes met verschillende afmetingen.
Er zijn ringetjes van drie verschillende formaten in verwerkt.
De goudsmid beweert dat de drie soorten ringetjes dezelfde hoeveelheid goud bevatten
(d.w.z. dezelfde oppervlakte hebben) omdat de koorden [AB], [CD] en [EF] dezelfde lengte hebben.

Heeft de goudsmid gelijk?

Tip. De stelling van Pythagoras toepassen.
Antwoord in bijlage

Bijlagen:
WISKUNDE BIJ DE GOUDSMID - oplossing.pdf (59.2 KB)   

NIEUWE (?) EIGENSCHAP VAN ZEVEN EN DERTIEN


Niet enkel in sprookjes komt het cijfer 7 af en toe voor
maar ook in de wiskunde blijkt het aantrekkelijke eigenschappen te bezitten.

We vermelden hier een nieuwe (?) eigenschap
waarvoor we in bijlage ook een bewijs geven.

Zoek een getal van 6 cijfers dat deelbaar is door 7.
We beweren dat elk getal dat je bekomt
via een cyclische permutatie van de cijfers van dat getal
ook weer deelbaar is door 7.

Voorbeeld. 
364 175 = 7 x 52 025.



Via cyclische permutatie bekom je dan
641 753 = 7 x 91 679
417 536 = 7 x 59 648
175 364 = 7 x 25 052
753 641 = 7 x 107 663
536 417 = 7 x 76 631.

Uit het bewijs (zie bijlage) volgt dat deze eigenschap ook geldig is voor het priemgetal 13.
Zo is 635 921 = 13 x 48 917.
Controleer nu zelf eens dat de getallen
359 216, 592 163, 921 635, 216 359 en 163 592
ook weer deelbaar zijn door 13. 

Test nu zelf eens of de eigenschap geldig is
voor een getal van 3 cijfers dat deelbaar is door 37.

Bijlagen:
EIGENSCHAP VAN 7.pdf (166.2 KB)   

MIJN UURWERKPARADOX



Om ongeveer 5 voor 12 en 5 na 12
maken de grote en de kleine wijzer van een uurwerk een hoek van 30°.
Hoeveel keer maken de twee wijzers dan elke dag
tussen middernacht en 12 uur 's middags een hoek van 30°?

Een simpele redenering is de volgende.
Ongeveer om 00.05 uur is er voor de eerste keer een hoek van 30° tussen beide wijzers.
Daarna is er rond elk uur telkens 2 keer een hoek van 30°
(ongeveer om 00.55 uur en ongeveer om 1.05 uur,
ongeveer om 2.05 uur en ongeveer om 2.15 uur enzovoort ...).
Ongeveer om 11.55 uur is er voor de laatste keer een hoek van 30°.
Dit geeft in totaal 1 + (11 x 2) + 1 = 24 keer.

Waar zit de fout in deze redenering?

28-04-2013 om 00:00 geschreven door Luc Gheysens  

Bestaat er een verband tussen de getallen pi en phi?



In de bijlage bewijzen we de volgende formule:





Verrassend toch ?
Pi is immers geen oplossing van een vierkantsvergelijking met gehele coëfficiënten
(pi is een transcendent irrationaal getal) terwijl phi dat wel is (phi is een algebraïsch irrationaal getal).



PI en PHI: om van te genieten!

Bijlagen:
Een merkwaardig verband tussen pi en phi.pdf (164.2 KB)   

Archimedes' Laboratorium is een boeiende en uitdagende website
die elke maand een wiskundig probleem lanceert.
Zie: http://www.archimedes-lab.org/ bij de rubriek 'Monthly Puzzle'.

We troffen er een ogenschijnlijk eenvoudige puzzel aan 
die ook een simpele en creatieve oplossing heeft.

PUZZEL 131
G is een willekeurige punt binnen een gelijkzijdige driehoek ABC.
Projecteer G loodrecht op de drie zijden en verbind G met de drie hoekpunten.
Dan ontstaan zes driehoeken (figuur 1).
Toon aan dat de som van de oppervlakten k + m + o
gelijk is aan de som van de oppervlakten l + n + p.

  Figuur 1

BEWIJS.
Trek door G een evenwijdige met de drie zijden van driehoek ABC.
De driehoek wordt dan verdeeld in drie parallellograms en drie gelijkzijdige driehoeken.
De lijnstukken die G met de hoekpunten A, B en C verbinden
verdelen deze parallellograms en deze gelijkzijdige driehoeken
telkens in twee delen met dezelfde oppervlakte.
Dan is
k + m + o = (x + a) + (y + b) + (z + c)
= (a + y) + (b + z) + (c + x) = l + n + p.

Q.E.D.

Figuur 2

24-04-2013 om 00:00 geschreven door Luc Gheysens  

KETTINGBREUKEN

Een kettingbreuk is één van die zonderlinge vondsten waarover men zich als wiskundige kan verbazen.

Een kettingbreuk is in feite een breuk in een breuk in een breuk in een breuk...
Er verschijnt telkens een breuk met teller 1
en in de noemer een geheel getal vermeerderd met een breuk met als teller 1
en dit herhaalt zich steeds weer.

Elk irrationaal getal is te schrijven als een oneindig lange kettingbreuk.

Zo ziet de kettingbreuk voor het getal π er uit:

En er bestaan ook nog een andere voorstellingen
waarin de kwadraatgetallen op een verrassende manier opduiken:

En dit is de kettingbreuk voor het getal φ (gulden snede):

In 2010 promoveerde Ionica Smeets (één van de wiskundemeisjes) aan de Universiteit van Leiden
via een doctoraatsthesis 'On continued fraction algorithms'.
Je vindt de tekst in bijlage.
Op p. 109-111 lees je hoe je zelf de kettingbreuk voor pi
(of een ander iarrtionaal getal) kunt vinden.
Meteen een leuke oefening voor in de wiskundeles!

Bijlagen:
Thesis Ionica Smeets - Kettingbreuken.pdf (5.5 MB)   

Ontdek jouw leerstijl

David A. Kolb is een gerespecteerd leerpsycholoog en pedagoog
die o.a. een studie maakte over de leerstijlen van leraars.
Hij kwam hierbij tot de conclusie dat er vier grote leerstijlen kunnen afgebakend worden:
er zijn doeners, dromers, denkers en beslissers.


Op http://www.123test.nl/leerstijl/ 
kan je via een eenvoudige test te weten komen
tot welk type jij behoort.
Zeker eens doen!

Zelf blijk ik tot het type 'denker' te behoren.
Wellicht typisch voor heel veel wiskundigen ...

 

In het tijdschrift BREEDBEELD van het VVKSO
verscheen deze maand een artikel
van de hand van collega Geert Delaleeuw en mezelf
waarin we o.a. verwijzen naar de diverse leerstijlen.
Het volledige artikel
met 7 tips voor de leerlingen
en 7 tips voor de leraar
voor het verwerven van wiskundige competenties
vind je in bijlage.
Met dank aan hoofdredacteur en collega Marleen Lippens.


Info en abonnementen: http://ond.vvkso-ict.com/vvksomainnieuw/document.asp?DocID=2442

Het is belangrijk jouw leerlingen te kennen
maar wellicht is het even belangrijk te weten wie je zelf bent!

Bijlagen:
Wiskunde in BREEDBEELD.pdf (1.6 MB)   

Regelmatige patronen en symmetrische figuren
oefenen vaak een magische aantrekkingskracht uit op wiskundigen.

Een mooi voorbeeld hiervan is een enneagram
(uit het Grieks: ennea is negen en gramma is tekening).
Via een regelmatige negenhoek stelt men in de pseudo-psychologie negen mogelijke persoonlijkheidstypes voor
en de pijlen ertussen symboliseren de onderlinge interactie tussen deze karaktertypes.

De negen types verhouden zich in een gestructureerde wijze tot elkaar.
Als iemand ontspannen en effectief is (in veilige omstandigheden)
neemt hij de goede eigenschappen van een bepaald ander type over (in de onderstaande figuur tegen de pijlen in)
en als iemand juist gespannen is (in stressvolle omstandigheden)
neemt hij de slechte eigenschappen van weer een ander type over (met de pijlen mee).

Op http://www.locomotiva.nl/test.php
kan je via een test ontdekken tot welk type jij behoort.

Hieronder zie je het resultaat van de test die ik vandaag zelf heb afgelegd...

Wist je dat ...
men een regelmatige negenhoek niet correct kan construeren 'op de Griekse wijze', d.w.z. met passer en liniaal
... en dat een regelmatige zevenhoek de veelhoek is met het kleinste aantal zijden waarvoor dit niet lukt ?

Een fraai resultaat over regelmatige veelhoeken is de volgende stelling:

Neem op een cirkel met straal 1 n punten die de cirkel in n bogen met dezelfde lengte verdelen.
Verbind één van de punten met de overige n-1 punten.
Dan is het product van de lengtes van deze n-1 koorden gelijk aan n.

In bijlage vind je een bewijs waarbij we gebruik maken van complexe getallen.

Bijlagen:
Stelling over een regelmatige n-hoek.pdf (206.7 KB)   

DE VLAG VAN TOGO

Als men twee vlaggen van de Afrikaanse republiek Togo 
 naast elkaar ophangt zoals op de bovenstaande afbeelding
dan blijken de punten A, B en C op één rechte lijn te liggen.

Wat betekent dat dan voor de verhouding van de lengte tot de breedte van deze vlag?

Via de stelling van Thales komen we tot een merkwaardig besluit:

De verhouding van de lengte tot de breedte van de vlag van Togo
is precies gelijk aan het getal  φ van de gulden snede (met φ ≈ 1,618).

Op wikipedia vonden we de juiste afmetingen van die vlag:
lengte = 80,9 cm en breedte = 50 cm en 80,9 : 50 = 1,618. 

15-04-2013 om 00:00 geschreven door Luc Gheysens  

Vandaag 15 april zet de doodle van Google Leonhard Euler (1707-1783) in de kijker.
Deze veelzijdige en geniale wiskundige werd op 15 april in Bazel geboren.

De doodle verwijst o.a. naar het feit dat Euler de basis legde voor de grafentheorie
via het gekende probleem van de 7 bruggen van Königsberg,
naar de formule e^{i x} = cos x + i sinx
en naar de formule V – E + F = 2
die een verband legt tussen het aantal hoekpunten (V = Vertices),
het aantal ribben (E = Edges) en het aantal zijvlakken (F = Faces)
van een willekeurig convex veelvlak.

Wie zich wil verdiepen in de grafentheorie
vind in bijlage de cursus van collega Fabien Decruyenaere (met dank!)
die op de voorbije Dag van de Wiskunde in Kortrijk hierover een lezing gaf.

Wie meer houdt van veelvlakken
dagen we uit om de volgende twee problemen op te lossen.

         

Welke van de 4 figuren op de linkse afbeelding is de ontvouwing van een kubus?
En welke van de 4 figuren op de rechtse afbeelding is de ontvouwing van het afgebeelde prisma?
Bron: New Puzzle Quizzes Deluxe (app)

Bijlagen:
Grafen naar grafen - syllabus.pdf (211.4 KB)   

 
Een perfect of volmaakt getal is een natuurlijk getal
dat gelijk is aan de som van zijn delers, het getal zelf niet meegerekend.

De kleinste twee volmaakte getallen zijn 6 en 28:
6 = 1 + 2 + 3 en 28 = 1 + 2 + 4 + 7 + 14.

Vermoedelijk maakten de oude Egyptenaren al studies van perfecte getallen.
Het is bekend dat Pythagoras perfecte getallen onderzocht.
Perfecte getallen hadden in die tijd een religieuze status.
In de beginjaren van het christendom bijvoorbeeld was er een theorie
dat de getallen 6 en 28 door God gekozen waren als perfecte getallen:
6 is het aantal dagen waarin God de aarde had geschapen
en 28 het aantal dagen waarin de maan om de aarde draait.
De heilige Augustinus (354-430) schreef ooit:
Zes is geen perfect getal omdat God de aarde in zes dagen geschapen heeft,
maar God heeft de aarde in zes dagen geschapen omdat zes een perfect getal is.
Bron: wikipedia.

In de Elementen van Euclides (boek IX, proposite 36) duikt een verrassende stelling
die een verband geeft tussen volmaakte getallen en priemgetallen:
Als 2ⁿ – 1 een priemgetal is, dan is 2^n-1(2ⁿ  –  1) een volmaakt getal.
Bewijs in bijlage.


Om de betekenis van deze stelling te begrijpen
volstaat het sommen van opeenvolgende machten van 2 (2⁰ = 1, 2¹ = 2, 2² = 4 ...) te bekijken:
 
1 + 2 = 3 is een priemgetal en daarom is 3 x 2 = 6 een volmaakt getal.
1 + 2 + 4 = 7 is een priemgetal en daarom is 7 x 4 = 28 een volmaakt getal.
1 + 2 + 4 + 8 = 15 is geen priemgetal en 15 x 8 = 120 geen volmaakt getal.
1 + 2 + 4 + 8 + 16 = 31 is een priemgetal en daarom is 31 x16 = 496 een volmaakt getal.

Kan je nu zelf het vierde volmaakt getal vinden?


 

Bijlagen:
Volmaakte getallen en priemgetallen - bewijs stelling.pdf (194.8 KB)   

HELIX EN CYCLOÏDE




Een helix (schroeflijn) ontstaat wanneer een punt
een eenparige cirkelbeweging uitvoert
in combinatie met een eenparige rechtlijnige beweging
in een richting die daar loodrecht op staat.



Een cycloïde ontstaat wanneer een punt beweegt op een cirkel
die rolt zonder glijden over een horizontale rechte lijn.

In een artikel dat verscheen in de Nieuwe Wiskrant
wijst Martin Kindt op een mooi verband tussen beide krommen.
De cycloïde (vlakke kromme) blijkt namelijk een projectie te zijn van de schroeflijn (ruimtekromme).
Lees hiervoor het artikel in bijlage.

Bijlagen:
Helix en cycloIde - Martin Kindt.pdf (21.6 KB)   

Het Wiskundetijdschrift Pythago­ras is onlangs begon­nen met een Face­bookpa­gina.

Op deze pagina zijn o.a. te vinden:
- Kleine Nootjes: wekelijks een uitdagend wiskundepuzzeltje
- Opgaven uit de Pythagoras-Olympiade
- Samenvattingen van artikels uit Pythagoras
- Wiskundenieuwtjes
- Lezersrubriek: bijdrage van leraars en docenten (bv. GeoGebra-constructies).

Facebookpagina: http://www.facebook.com/Pythgrs?ref=hl

            Pythagoras: verdraaid leuk!

PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

Kan je dit nootje kraken?

BROERS EN ZUSSEN

De moeder van David en Susan is in verwachting van een baby.
Als het een meisje is, heeft David tweemaal zoveel zussen als broers.
Maar als het een jongetje is, dan heeft Susan tweemaal zoveel broers als zussen.

Hoeveel kinderen heeft moeder (zonder het kind waarvan ze in verwachting is)?

PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

14-04-2013 om 00:00 geschreven door Luc Gheysens  

WISKUNDE EN BLOKKEN

Ben Crabbé presenteert vandaag (zaterdag 13 april 2013) op TV-één de 4000-ste aflevering van BLOKKEN.

Naast de quiz-vragen speelt TETRIS een centrale rol in het populaire spelprogramma Blokken.
Dit beroemde spelletje wordt gespeeld met 7 verschillende figuren (blokken)
die elk uit 4 vierkantjes zijn opgebouwd.
Het zijn de zogenaamde TETROMINO's,
een veralgemening van de domino-blokken.
Met een beetje verbeelding ziet men dat de 7 figuren
de vorm hebben van de letters Z, S, O, T, J, L en I.

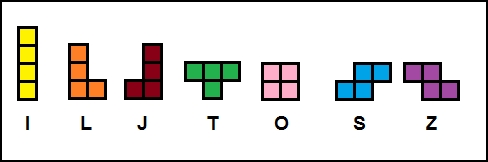
Merk op dat de Z- en S-blokken congruent zijn en ook de J- en L-blokken.
Ze zijn immers telkens elkaar spiegelbeeld.
Daarom noemt men de vijf onderstaande vlakke figuren ook soms de vrije tetromino's.

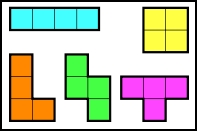
DENKOEFENING.
Kan je bewijzen dat je met deze vijf figuren geen 4 x 5-rechthoek kunt vormen?

Oplossing in bijlage.



Een wiskundelerares uit Bree
keek trouw naar Blokken op TV.
Ze was  verliefd (nogal fel)
op het boeiende tetris-spel
en ook wel een beetje op Ben Crabbé.

Bijlagen:
Tetromino-probleem opgelost.pdf (48.8 KB)   

M-LEARNING

 

KATHO is de eerste hogeschool in de Benelux
met een eigen iTunes U-site

KATHO, de Katholieke Hogeschool Zuid-West-Vlaanderen,
is de grootste instelling voor hoger onderwijs in West-Vlaanderen,
en is de eerste onderwijsinstelling in de Benelux met een eigen iTunes U-site.
iTunes U is een innovatieve manier om hoorcolleges, lessen, podcasts
en nog heel wat meer te distribueren zodat studenten
- maar ook mensen die niet aan de instelling zijn verbonden -
vanaf afstand toegang hebben tot een zeer breed aanbod informatie.

Is het tijdperk van het mobiel leren definitief aangebroken?
Meer informatie op https://www.apple.com/benl/education/real-stories/

Onlangs verdedigde Joke Coens aan de KU Leuven Kulak
haar doctoraatstproefschrift "Mobile learning in higher education. The multitasking issue".
Hierin onderzoekt ze diverse aspecten van het mobiel leren.
Lees in dit verband  het artikel op http://nieuws.kuleuven.be/node/11690 .

Een groep studenten uit Kiel
vond dat stil zitten wat tegenviel.
Met heel wat kabaal
verlieten ze de studiezaal.
Sindsdien leren ze mobiel.

12-04-2013 om 00:00 geschreven door Luc Gheysens  

In zijn boek Underweysung der Messung (1525)
schetst Albrecht Dürer een zij-aanzicht van een wenteltrap
en zonder het zelf te beseffen 
tekent hij hiermee wellicht de oudst bekende afbeelding van een sinusoïde.

Dit is één van de vele weetjes uit het genietbare boek
Wiskunde, dat kun je begrijpen!
van de Nederlandse wiskundepioniers
Martin Kindt en Ed de Moor.

Moet je gelezen hebben!

 

In het boek vonden we ook een leuke oefening over driehoeksgetallen.
Op de onderstaande figuur staan de eerste 6 driehoeksgetallen
en ook de formule voor het n-de driehoeksgetal T_n.
Merk op dat T_n = 1 + 2 + 3 + ... + n.


Bron: wikipedia.

Bekijk nu de volgende rij sommen:
1³  = 1, 1³ + 2³ = 9, 1³ + 2³ + 3³ = 36, 1³ + 2³ + 3³ + 4³ = 100 enzovoort.
Kan je aantonen dat de uitkomsten 1, 9, 36, 100 ...
telkens het kwadraat zijn van een driehoeksgetal
m.a.w. dat 1³ + 2³ + 3³ + ... + n³ = (1 + 2 + 3 + ... + n)² ?

Tweevoudig bewijs in bijlage.

Bijlagen:
Een visueel bewijs voor de formule.pdf (200.8 KB)   
Formule som van derdemachten.pdf (217.1 KB)   

WISKUNDE MET STRAUSS

Een wiskundestudent uit Meadows
begreep niets van de theorie van Gauss.
Van statistiek werd hij ziek.
Nu studeert hij muziek
en geniet van de walsen van Strauss.

Maar weet jij waarom men de breuk 41/333
het André Rieu-getal noemt?
Je krijgt een Radetzky-mars bedenktijd.
Tip. Bereken eens de breuk met een rekentoestel.

Bron: www.rekenbeter.nl - Doordenker van 13 november 2012

12-04-2013 om 00:00 geschreven door Luc Gheysens  

Wanneer je aan een student vraagt om een curve met lengte π te tekenen,
dan zal hij wellicht direct denken aan een cirkel met straal 1.
Maar hoe teken je een curve met lengte π² ?

De oplossing is te vinden via een verrassende kromme. 

DE AFWIKKELKROMME

Deze kromme ontstaat door het traject te volgen van het eindpunt van een stuk touw
dat je afwindt van aan cirkelvormige klos waarbij je het touw goed gestrekt houdt.
In wiskundige vaktaal spreekt men van de cirkelevolvente.



Applet - bron: wikipedia

Wanneer de klos een diameter van 4 cm heeft
en je de draad over een hoek van 180° afwindt,
dan beschrijft het eindpunt een curve met lengte π².

Deze figuur met het bijhorend rekenwerk vind je in de bijlage.

Bijlagen:
Parametervergelijkingen van de cirkelevolvente - berekening.pdf (189.8 KB)   

Hoe teken je een curve met lengte π² ?

Wanneer je aan een student vraagt om een curve met lengte π te tekenen,
dan zal hij wellicht direct denken aan een cirkel met straal 1.
Maar hoe teken je een curve met lengte π² ?

De oplossing is te vinden via een verrassende kromme. 

DE AFWIKKELKROMME
ontstaat door het traject te volgen van het eindpunt van een stuk touw
dat je afwindt van aan cirkelvormige klos waarbij je het touw goed gestrekt houdt.
In wiskundige vaktaal spreekt men van de cirkelevolvente.



Applet - bron: wikipedia

Wanneer de klos een diameter van 4 cm heeft
en je de draad over een hoek van 180° afwindt,
dan beschrijft het eindpunt een curve met lengte π².
Hieronder zie je een figuur die ik met de TI-Nspire App heb getekend.
Op de figuur staan de parametervergelijkingen van de curve vermeld.
De curve met lengte π² begint in het punt (2,0) en eindigt in het punt P(-2, 2π)
Het rekenwerk vind je in de bijlage.
 


Via het onderstaande filmpje kan je zien hoe een afwikkelkromme
(in omgekeerde zin) kan getekend worden.

Bijlagen:
Parametervergelijkingen van de cirkelevolvente.doc (102 KB)   

PRIEMGETALLEN BLIJVEN WISKUNDIGEN FASCINEREN

 

Op 25 januari 2013 kwam de melding dat er een nieuw grootste priemgetal was gevonden:

The record is currently held by 2^{57 885 161} − 1 with 17 425 170 digits.
Its discovery resulted from the Great Internet Mersenne Prime Search (GIMPS).

Hoe kent men het exacte aantal cijfers van dit immens groot priemgetal p?
Neem de tiendelige logaritme van p+1:
log (p+1) = 57 885 161 . log(2) = 17 425 169,7648...
Als de logaritme van een natuurlijk getal g tussen de twee opeenvolgende gehele waarden k–1  en k ligt,
 betekent dit dat het getal zelf tussen 10^k-1  en 10^k  ligt en bijgevolg heeft het getal g dan k cijfers.

Wat is het cijfer van de eenheden van het grootst gekende priemgetal?
Dat getal eindigt op het cijfer 1.
Verklaring. Als de exponent bij het grondtal 2
een viervoud +1 is, dan eindigt het getal op het cijfer 2.

PRIEMTOETJE
Dit zijn de priemgetallen tot en met 71:
2   3   5   7   11   13   17   19   23   29   31   37   41   43   47   53   59   61   67   71
 De 19 oneven priemgetallen uit dit lijstje (2 is het enige even priemgetal)
kan men in een merkwaardige stervormige figuur plaatsen
 zodat de som van de 5 priemgetallen op elke lijn gelijk is aan 167.
En 167 is zelf weer een priemgetal. Wonderbaar!

MIJN PRIEMGETALLENSTELLING.
Als men 5 optelt bij even macht van een priemgetal groter dan 3
bekomt men steeds een getal dat deelbaar is door 6.

Twee voorbeelden. 
7⁸ + 5 = 5 764 806 en  13⁶ + 5 = 4 826 814 
Dit zijn telkens even getallen waarvan de som van cijfers een 3-voud is.
Ze zijn bijgevolg deelbaar door 6.

Een bewijs zit in bijlage.

Bijlagen:
MIJN PRIEMGETALLENSTELLING.pdf (128.3 KB)