Dit zijn twee merkwaardige formules om ln 2 te berekenen.

Volgens de eerste sommatieformule is ln 2 = 1 – 1/2 + 1/3 –  1/4 + 1/5 – 1/6 + ....
Deze formule volgt uit de Maclaurinreeks voor f(x) = ln(1 + x),
nl.  ln(1 + x) = x – x/2 + x/3 – x/4 + x/5 – x/6 + ... waarin men x = 1 stelt.

Volgens de tweede formule is ln 2 = 1/2 + 1/12 + 1/30 + 1/56 + ...
waarbij de noemers van de breuken achtereenvolgens gelijk zijn aan
1 x 2, 3 x 4, 5 x 6, 7 x 8, enzovoort.
Dat deze formule gelijk is aan de eerste uitdrukking volgt direct uit het feit
dat 1/((2n+1)(2n+2)) = 1/(2n+1) – 1/(2n+2).

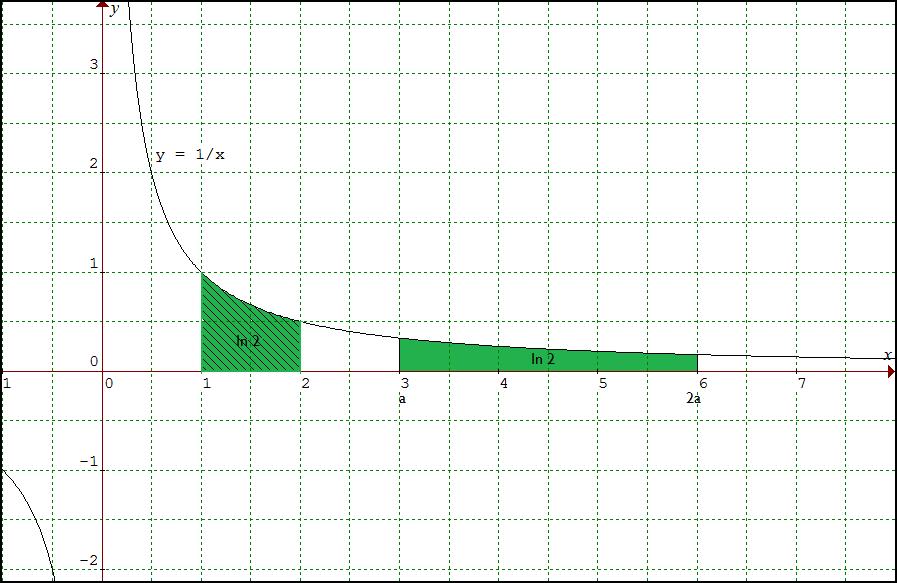
Het merkwaardig getal ln 2 is ook gelijk aan het maatgetal van de oppervlakte
van het vlak gebied tussen de grafiek van f(x) = 1/x en de x-as
tussen de verticale rechten x = 1 en x = 2,
maar ook tussen de verticale rechten x = a en x = 2a (met a > 0).

Deze eigenschap controleert men direct via een bepaalde integraal:

14-07-2013 om 00:00 geschreven door Luc Gheysens  

       PI OP POSTZEGELS

2000 was het Internationaal Jaar van de Wiskunde.
Heel wat landen (waaronder België) brachten voor die gelegenheid een postzegel uit.
 Slechts op enkele ervan staat het getal π afgebeeld.
Hierboven zie je dat dit het geval was voor een postzegels van Monaco. 



Nikolai Luzin was een eminente Russische wiskundige die van 1920 tot 1930
aan de Universiteit van Moscou een onderzoeksseminarie leidde.
Heel wat doctoraatsstudenten werkten er onder zijn leiding
en een aantal ervan werden later beroemde Sovjet-wiskundigen.

   

De Vereniging van Colombiaanse Ingenieurs heeft een logo waarin het getal π staat afgebeeld. 

   

  

En vind je ook π op de bovenstaande  herdenkingszegels?




Op deze omslag met een bijzondere eerste-dag-afstempeling
staat een tekening van de grote piramide van Cheops
waarbij de afmetingen ervan in verband worden gebracht met het getal π.

En blijkbaar zijn de postzegels waarop het getal e (getal van Euler e = 2,71828...)
staat afgebeeld nog veel zeldzamer!

 

   

 

In 1998 vond in Berlijn een Internationaal Wiskunde Congres plaats.
Er verscheen toen een postzegel waarin een vierkant staat afgebeeld
dat zelf weer met vierkanten is opgevuld en op de achtergrond
zie je het getal pi met heel veel cijfers na de komma. 

Karl Weierstrass (1815-1897) wordt wel eens de vader van de moderne analyse genoemd.
Hij definieerde een functie die overal continu is, maar nergens differentieerbaar.
In de definitie van de functie van Weierstrass komt het getal π voor.



Augustin Cauchy (1789-1857) was een Franse wiskundige
die de basis legde voor de complexe functietheorie.
Hij bewees o.a. een formule voor een kringintegraal waarin het getal π opduikt.
Die formule van Cauchy staat bovenaan op de herdenkingszegel afgebeeld.

               

10-07-2013 om 00:00 geschreven door Luc Gheysens  

Dit jaar waren er 5 289 studenten ingeschreven voor deelname 
aan het toelatingsexamen voor arts en tandarts, dat sedert 1997 bestaat.
Dit is een toename met 11 % in vergelijking met vorig jaar.
Bijna 1 op 5 deelnemers komt uit Nederland.
Opvallend is dat bijna 600 deelnemers uit het vijfde jaar komen.
De proef werd op 2 juli 2013 georganiseerd in Brussels Expo.

Vorig jaar slaagde 16,6 procent (1 op 6) in de zittijd van juli.

En zopas zijn ook de resultaten bekend van de eerste zittijd van dit jaar.
Van de 5 289 ingeschreven kandidaten legden 4 737 studenten, of 89,5 procent, het volledige examen af.
Na deliberatie slaagden 695 kandidaten. Dit aantal is iets lager dan in juli vorig jaar (712 in juli 2012).
Door het gestegen aantal deelnemers (er waren 4 301 deelnemers in juli 2012)
is het slaagpercentage voor juli 2013 daarom 14,7 procent van de deelnemers.
Als we echter ook de studenten meetellen die niet het volledige examen hebben afgelegd
komen op een een slaagpercentage van 13,1 procent of bijna 1 op 8.
Van de vijfdejaarsstudenten die deelnamen slaagde 1,2 procent.

Neem je nog even de tijd voor een wiskundig examenvraagstuk?

Birgit nam dit jaar deel aan het toelatingsexamen voor arts en tandarts.
Ze was één van de 49 deelnemers in vak 23.
De studenten in dit vak waren genummerd van 1 tot en met 49.
Birgit stelde iets merkwaardigs vast:
de som van de nummers die kleiner waren dan haar nummer
was precies gelijk aan de som van de nummers die groter waren dan het hare.
Welk nummer had Birgit?



Oplossing in bijlage.

Bijlagen:
Oplossing examenraadsel.pdf (200.2 KB)   

 
Neem er even een blad papier en een balpen bij voor een cijferwerkje.

STAP 1.  Kies jouw lievelingscijfer uit de rij 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9.
STAP 2.  Vermenigvuldig het gekozen cijfer (uit het hoofd!) met 9.                                
 STAP 3.  Vermenigvuldig nu (manueel!) het bekomen getal met het getal 12 345 679.  

Tevreden met de uitkomst?

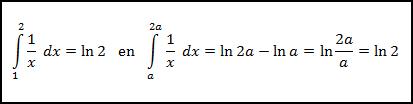
08-07-2013 om 00:00 geschreven door Luc Gheysens