In een perfecte wereld ...
zou het bewijs van heel wat wiskundige stellingen
veel eenvoudiger moeten zijn.

Daarom stellen we hier een nieuw bewijs voor
van de stelling van Pythagoras.

De vlieger van Pythagoras

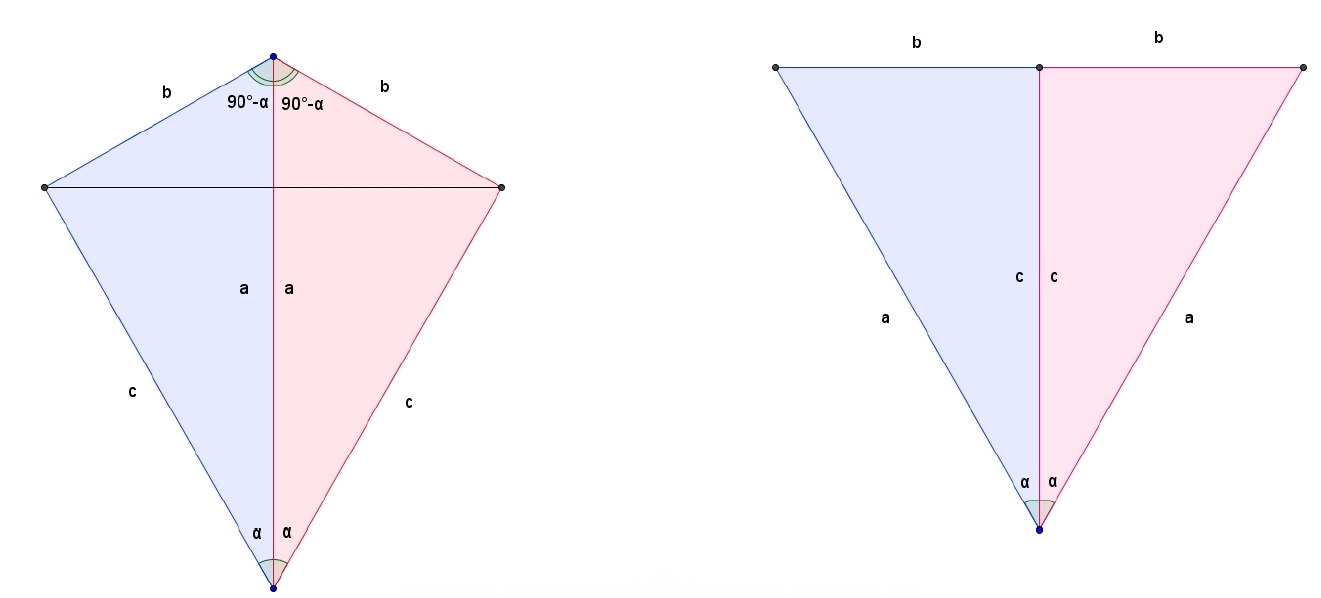
Op de linkse figuur staat een vierhoek afgebeeld die men een vlieger noemt.
Deze vlieger bestaat uit twee rechthoekige driehoeken.
Wanneer je deze twee driehoeken op een andere manier tegen elkaar plaatst,
bekom je de rechtse figuur, die een gelijkbenige driehoek is.
Uiteraard hebben beide figuren dezelfde oppervlakte.

Een gekende formule voor de oppervlakte van een driehoek is de volgende:
"De oppervlakte van een willekeurige driehoek is gelijk aan
het halve product van twee zijden vermenigvuldigd met de sinus van de ingesloten hoek".

Door deze formule op beide figuren toe te passen,
bekom je een vrij eenvoudig bewijs
van de stelling van Pythagoras.

Lees de bijlage!

Op http://www.cut-the-knot.org/pythagoras/index.shtml
heeft professor Alexander Bogomolny (University of Iowa)
heel wat bewijzen verzameld.

De Engelstalige uitleg over 'de vlieger van Pythagoras'
vind je op http://www.cut-the-knot.org/pythagoras/Proof80p.shtml.

Bijlagen:
De vlieger van Pythagoras - bewijs.pdf (224.6 KB)