|
Infinity
kalligrafisch uitgebeeld door Kim Scott
STELLING. Op een lijnstuk liggen evenveel punten als op een rechte.
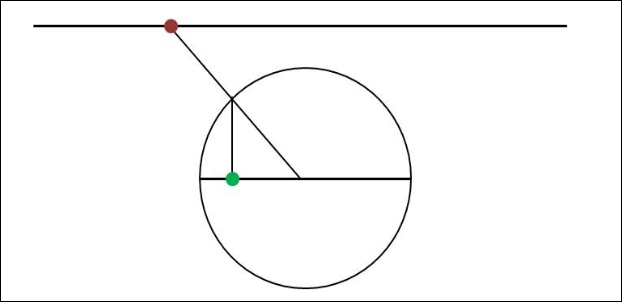
Op de onderstaande figuur zie je dat er met elk groen punt op de middellijn van de cirkel
precies één rood punt van de getekende rechte correspondeert en omgekeerd.
Het volstaat immers via een lijnstuk een willekeurig rood punt op de rechte
te verbinden met het middelpunt van de cirkel
en vervolgens het snijpunt van dat lijnstuk met de cirkel
loodrecht te projecteren op de middellijn van de cirkel.
Die projectie levert dan een groen punt op.
STELLING. Er zijn evenveel natuurlijke getallen als er gehele getallen zijn,
m.a.w. in de verzameling {0, 1, 2, 3, ...} zitten evenveel getallen als in {...,-3, -2, -1, 0; 1, 2 , 3, ...}.
Dit kan je gemakkelijk als volgt inzien.
Met een even natuurlijk getal n en laten we het positief geheel getal n/2 overeenkomen.
Met een oneven natuurlijk getal n laten we het negatief geheel getal -(n+1)/2 overeenkomen.
Zo komt met elk natuurlijk getal precies één geheel getal overeen en omgekeerd.
 
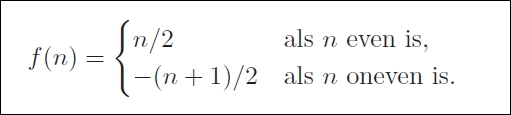
Het duurde tot in de 19de eeuw tot wiskundigen een juist begrip hadden van 'oneindig veel'.
De wiskundigen Georg Cantor en David Hilbert leverden op dit vlak baanbrekend werk
en kwamen tot de conclusie dat de verzamelingen van de natuurlijke getallen,
van de gehele getallen en van de rationale getallen 'aftelbaar oneindig' veel elementen bevatten,
terwijl dat voor de verzameling van de reële getallen niet waar is:
 (alef-nul) ≠  (alef-één)
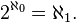
Een goed bewaard geheim van Georg Cantor
(lees meer hierover in de bijlage).
Over het werk van Cantor verneem je ook meer op
http://www.math4all.nl/Wiskundegeschiedenis/Wiskundigen/Cantor.html
In het volgende filmpje leer je dat ∞ + 1 = ∞ en dat 2 ∞ = ∞
wat aanleiding gaf tot de paradox van het Hilberthotel.
 Bijlagen:
Oneindig Robbert Dijkgraaf.pdf (765.6 KB)
14-12-2013 om 00:00
geschreven door Luc Gheysens 
|
In de bijlage zit een variatie op deze 'stelling'
