Op 5 augustus 1962 - precies 50 jaar geleden - overleed Marilyn Monroe.
Voor veel mannen is en blijft ze een sexy vrouw met de ideale maten:
89 - 55 - 89 (in cm)
of 35" - 22" - 35" (1" = 1 inch = 2,54 cm).

Bestaat er een verband tussen 'de ideale maten' van Marilyn en 'de gulden snede'?
Het getal van de gulden snede is φ = 1,618 ... en  89/55  = 1,618 ...
De getallen 89 en 55 zijn ook twee opeenvolgende getallen uit de rij van Fibonacci!

********************************

In een recent statistisch onderzoek vroeg men aan 3000 vrouwen welke figuur ze zelf hadden.
Dit waren de resultaten:
* 27% het ‘butternut’-pompoenfiguur, beter bekend als de zandloper: smalle taille, brede heupen en grote borsten,
* 21% een peerfiguur: smalle taille, kleine borsten, brede heupen
* 21% het appelfiguur: rondom rond, ook aan de taille en de boezem
* 16% beschreef zichzelf als een aubergine: een brede taille en brede heupen
* 15% vond zichzelf een wortel: lang en smal, zonder rondingen of een broccoli: grote boezem, smalle taille en smalle heupen.

Nochtans blijken steeds minder vrouwen een zandloperfiguur te hebben.
De 'norm' is momenteel dat de verhouding tussen de taille en de heupomtrek 0,7 is.
Dit vinden de mannen blijkbaar het meest aantrekkelijk!

******************************************

Bekijk nu even de onderstaande foto.
Van dichtbij blijkt het een foto van Einstein te zijn.
Ga dan op 5 meter van jouw computerscherm staan.
Zie je nu Marilyn?

05-08-2012 om 00:00 geschreven door Luc Gheysens  

 

Elders op mijn blog kan je lezen waar je het getal φ van de gulden snede terugvindt in een regelmatige vijfhoek.

Zo is op de bovenstaande figuur |AB| / |BG| = φ

De vraag is nu of φ ook in verband staat met een gelijkzijdige driehoek en een vierkant.
Hieronder lees je dat het antwoord op deze vraag positief is!

1. De gulden snede bij een gelijkzijkdige driehoek en de omgeschreven cirkel.

 

A en B zijn de middens van de twee zijden van de gelijkzijdige driehoek.
AB snijdt de cirkel in een punt G.

Dan is  |AB| / |BG| = φ.

Hint voor het bewijs: gebruik de macht van het punt B t.o.v. de cirkel. 

2. De gulden snede bij een vierkant geconstrueerd op de middellijn van een cirkel.

 

Een vierkant wordt geconstrueerd op de middellijn van een cirkel
zoals op de bovenstaande figuur.
A en B zijn de twee hoekpunten van het vierkant die op de middellijn AB liggen.
De andere twee hoekpunten van het vierkant liggen op de cirkel.
AB snijdt de cirkel in een punt G.

Dan is |AB| / |BG| = φ.

Hint voor het bewijs: gebruik de macht van het punt B t.o.v. de cirkel
en de stelling van Pythagoras.

Meer uitleg in de bijlage!

Bijlagen:
Gulden snede bij driehoek en vierkant.pdf (163.9 KB)   

Om te leren tellen gebruikt men vanaf het kleuteronderwijs allerlei hulpmiddeltjes zoals kinderliedjes en aftelrijmpjes.

                     DE ZEVENSPRONG

           Een kleuterjuffrouw uit Bergen
           kon haar voorliefde voor 7 niet verbergen.
           De zevensprong danste ze enthousiast
           en dagelijks keken haar kleuters klokvast
           naar 'Sneeuwwitje en de 7 dwergen'.
                                                          L.G.


           TIEN KLEINE NEGERTJES 
           gebaseerd op de meest succesvolle misdaadroman van Agatha Christie (1939)

                              

10 kleine negertjes gingen uit eten langs verre wegen.

1 stikte in zijn drankje – toen waren er nog 9.

9 kleine negertjes praatten tot diep in de nacht,

1 kon niet wakker worden – toen waren er nog 8.

8 kleine negertjes kwamen op een eiland aangedreven,

1 zei, dat hij niet verder wou – toen waren er nog 7.

7 kleine negertjes kapten hout met een kapmes,

1 sloeg zichzelf in tweeën – toen waren er nog 6.
 

6 kleine negertjes hielden een honingbedrijf,

Eén werd gestoken door een bij – toen waren er nog 5.

5 kleine negertjes kregen met het recht gemier,

Eén kwam terdege in de knoei – toen waren er nog 4.
 

4 kleine negertjes gingen naar zee en zie,

Eén rode haring verzwolg er een – toen waren er nog 3.

3 kleine negertjes gingen naar Artis mee,

Eén grote beer drukte er een fijn – toen waren er nog 2.
 

2 kleine negertjes gingen naar het zonnebad heen,

1 schroeide de zon een gat in zijn bast – toen was er nog maar 1.

1 klein negertje bleef helemaal alleen.

Hij hing tenslotte zich maar op – dus bleef er toen niet één.

TELLEN EN SPELLEN MET EEN KAARTSPEL

Neem een spel van 52 kaarten.
Leg de 4 azen bovenop. Daaronder de 4 tweeën, dan de 4 drieën ... 4 tienen, 4 boeren, 4 dames en 4 heren.
Spel nu de volgende woorden:
EEN  TWEE   DRIE   VIER   VIJF   ZES   ZEVEN   ACHT  NEGEN   TIEN  BOER   DAME   HEER
en leg bij elke gespelde letter een kaart op tafel met de rugzijde naar boven.
Bij de rode letters draai je een kaart om  met de beeldzijde naar boven.
Deze kaart zal telkens precies de waarde hebben van het gespelde woord.

In plaats van EEN kan je natuurlijk ook AAS spellen.

Omdat je in totaal 52 letters hebt gespeld zal je ook op het einde alle kaarten hebben neergelegd!

04-08-2012 om 00:00 geschreven door Luc Gheysens  

Hallo rekenknobbel!
Neem er even een rekenmachientje bij.

Bereken het volgende product:
13 837  x (jouw leeftijd) x 73.

Verwonderd over de uitkomst?!
Maar kan je dit ook verklaren?

04-08-2012 om 00:00 geschreven door Luc Gheysens  

Jaren geleden kocht ik in Engeland het boekje 'MATHEMATICS MAGIC AND MYSTERY' van Martin Gardner.
Deze bijdrage is dan ook op de eerste plaats bedoeld als een eerbetoon aan Martin
die tientallen boekjes schreef over ludieke en leerrijke wiskunde.
Hij verzorgde ook 25 jaar lang de column Mathematics Games
in The Scientific American en toonde hiermee de opvoedende waarde aan
van wiskundige puzzels, spelletjes en goocheltrucs.



Martin Gardner (1914-2010)

In het hierboven vermelde boekje beschrijft Martin een aantal goocheltoeren met kaarten en getallen.
Op Youtube vond ik een 'verfilming' van een leuke variante op één van de beschreven trucs.
Hieronder kan je het filmpje bekijken.

De goochelaar laat eerst een vrijwilliger een willekeurig aantal kaarten van 1 tot en met 12 afnemen van de stapel.
De goochelaar ziet dus niet hoeveel de vrijwilliger er afneemt. Hij zal dit immers raden!
Dan telt de goochelaar 12 kaarten af van die stapel.
Hij legt ze daarna in de vorm van de 12 uren van een klok.
Meteen weet de goochelaar te zeggen hoeveel kaarten de vrijwilliger van de stapel heeft genomen.
Bovendien had de goochelaar blijkbaar vooraf op een briefje voorspeld welke kaart
precies op het uur zou liggen dat overeenkomt met het aantal afgenomen kaarten.

Verklaring.
In het filmpje had de goochelaar vooraf ruitenvier op positie 13 geplaatst.
De vrijwilliger neemt N kaarten af.
De goochelaar gebruikt nu de kaarten N+1, N+2  ... N+12,
maar keert hun volgorde om bij het aftellen van de kaarten van het hoopje.
Kaart N+12 zal hierdoor het uur 1 aanduiden,
kaart N+11 zal het uur 2 aanduiden,
enzovoort ... tot en met kaart N+1 die het uur 12 zal aanduiden.
Logisch dat kaart 13 dan het uur N zal aanduiden:
(N+12 + 1 = N+11 + 2 = ...= 13 + N)!



In de volgende bijdrage op mijn blog vind je een eenvoudige variante hierop
die eveneens in het hierboven vermelde boek van Martin Gardner wordt beschreven.

03-08-2012 om 00:00 geschreven door Luc Gheysens  

In zijn boek MATHEMATICS MAGIC AND MYSTERY
beschrijft Martin Gardner een eenvoudige goocheltruc met dierennamen.
Gebruik hiervoor de onderstaande afbeelding.
Printversie in bijlage.

Bijlagen:
Dieren-Tik-Truc.pdf (201.3 KB)   

            Mijn favoriete regelmatige veelhoek is de regelmatige zevenhoek.          

       Convexe regelmatige              De twee stervormige regelmatige 
    zevenhoek                                   zevenhoeken
 

Waarom?

1. Het is de regelmatige veelhoek met het kleinste aantal zijden die niet met een passer en een liniaal kan geconstrueerd worden.

2. Wist je dat  je wellicht dagelijks een regelmatige zevenhoek 'ontmoet'?
 

   De muntstukjes van 20 eurocent hebben immers 7 inkepingen in de rand en zo wordt een regelmatige zevenhoek uitgetekend.

3. Beschouw de driehoek ABC in de onderstaande regelmatige zevenhoek. 
   Als de zijden van deze driehoek als lengte a, b en c hebben, dan is

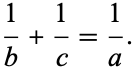
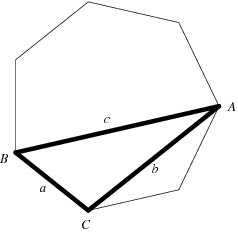
Voor het bewijs moet je eerst de stelling van Ptolemaeus (zie elders op mijn blog) toepassen in een vierhoek
(bepaald door 4 hoekpunten van de zevenhoek) met zijden c, a, a en b en met diagonalen c en b. 
Volgens de stelling van Ptolemaeus is ca + ab = cb.
Deel daarna de drie termen door abc en je vindt de vooropgestelde formule.
Zie ook:  http://www.qbyte.org/puzzles/p091ss.html . 

4. Omdat er 7 dagen zijn in een week, mag je verwachten dat er pillendoosjes bestaan in de vorm van een regelmatige zevenhoek.
    En ja hoor, we vonden zo een doosje op het internet.

02-08-2012 om 00:00 geschreven door Luc Gheysens  

   

Wist je dat je met een gewicht van 1 kg, van 3 kg en van 9 kg
alle mogelijke gehele gewichten (massa's) van 1 tot en met 13 kg kunt afwegen?
Merk op 3⁰ = 1,  3¹ = 3  en 3² = 9 zijn machten van 3.

Enkele voorbeelden.
We nemen aan dat je het af te wegen pak in de linkerschaal plaatst.
Om een pak van 6 kg af te wegen, plaats je bij dat pak 3 kg en plaats je dan 9 kg in de rechterschaal.
Om een pak van 5 kg af te wegen, plaats je bij dat pak 1 kg en 3 kg en weer 9 kg in de rechterschaal.
Om een pak van 4 kg af te wegen, plaats je gewoonweg 1 kg en 3 kg in de rechterschaal.

Ga na dat je zo alle gewichten van 1 kg tot en met 13 kg kunt afwegen.
En controleer ook eens dat je met een gewicht van 1 kg, 3 kg, 9 kg en 27 kg   (27 = 3³)
alle mogelijke gewichten van 1 kg tot en met 40 kg kunt afwegen.                      

30-07-2012 om 00:00 geschreven door Luc Gheysens