|

Fractalen blijven tot de verbeelding spreken van veel wiskundigen.
Een fractal kan je omschrijven als een meetkundige figuur
waarin eenzelfde motief zich op een steeds kleinere schaal herhaalt.
Met S duidt men de schaalfactor
waarbij 1/S de factor is waarmee de figuur telkens wordt verkleind.
N is het aantal kopieën van de oorspronkelijke figuur
die bij elke volgende stap aan de figuur wordt toegevoegd.
De dimensie D van een fractal is dan gedefinieerd door
SD = N
of ook via: D = log N / log S.
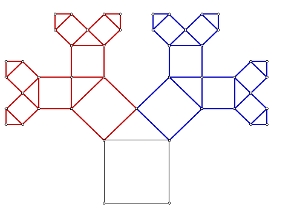
Voorbeeld. Bij de onderstaande Pythagorasboom is S = √2 en N = 2 zodat de dimensie D = 2.
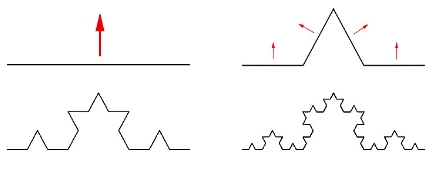
Hieronder zie je hoe de Kochkromme ontstaat.
Het wordt een kromme met een oneindige lengte
maar de oppervlakte onder de kromme
(in het groen aangeduid op de figuur bovenaan deze pagina)
is eindig.
Bij deze kromme worden telkens 4 kopieën gemaakt van de vorige figuur en worden de lijnstukjes 3 keer korter
De dimensie van de Kochkromme is bijgevolg D = log 4 log 3 ≈ 1,26.
De dimensie van de onderstaande driehoek van Sierpinski is gelijk aan
D = log 3/log 2 ≈ 1,585.

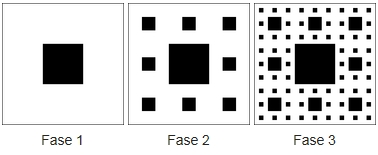
Voor het tapijt van Sierpinski vertrekt men van een vierkant (= fase 0)
en bekomt men als dimensie D = log 8/log 3 ≈ 1,8928.
De spons van Menger is een driedimensionale fractal waarbij het vertrekpunt (fase 0) een kubus is
en de dimensie is D = log 20/ log 3 ≈ 2,7268.

Dit onderwerp is uiteraard geschikt voor een wiskundige eindwerkje in het secundair onderwijs (zie bijlage). Bijlagen:
Fractale-dimensie_eindwerk-wiskunde.pdf (1 MB)
06-06-2012 om 00:00
geschreven door Luc Gheysens 
|
