De A-serie van papierformaten is een serie van vellen waarbij het eerstvolgende vel steeds een tweemaal zo grote (of kleine) oppervlakte heeft.

De verhouding tussen de lange en de korte zijde is zo, dat wanneer het vel over de lange zijde in twee wordt geknipt

(dus de oppervlakte gehalveerd), er twee kleinere rechthoeken onstaan die gelijkvormig zijn met de grotere rechthoek.

Dus als k de korte zijde en l de lange zijde van een blad papier uit de A-serie is,  geldt:

 
ofwel

 
ofwel

Hieruit blijkt dat de verhouding tussen de lange en korte zijde de vierkantswortel uit 2 is.

De serie begint met A0, een vel met een oppervlakte van 1 vierkante meter.

Met de berekende verhouding levert dat een vel op van 1189 mm bij 841 mm.

Door deling volgt hieruit de complete serie:

naam	lengte	breedte
A0	1189 mm	841 mm
A1	841 mm	594 mm
A2	594 mm	420 mm
A3	420 mm	297 mm
A4	297 mm	210 mm
A5	210 mm	148 mm
A6	148 mm	105 mm
A7	105 mm	74 mm
A8	74 mm	53 mm
A9	53 mm	37 mm
A10	37 mm	26 mm
A11	26 mm	18 mm

Kijk eens na of  postzegels ook een A-formaat hebben!

Hieronder zie je een leuke postzegel uit Australië waarop allusie wordt gemaakt op het verband tussen graden Celsius en graden Fahrenheit. 

Ken je de formule voor de omzetting van graden Celsius naar graden Fahrenheit (en omgekeerd)?

 

11-10-2009 om 00:00 geschreven door Luc Gheysens  

Dit jaar viert het wiskundetijdschrift Uitwiskeling zijn zilveren jubileum.

Reeds 25 jaar lang wil Uitwiskeling nieuwe ideeën aanreiken voor de klaspraktijk.

Dit tijdschrift van en voor leraren heeft ook een webstek: www.uitwiskeling.be. 

je vindt er o.a. een overzicht van alle vorige jaargangen, een korte beschrijving van de inhoud van de volgende nummers, applets en links naar andere sites.

Interessant zijn ook de werkbladen die de redactie ter beschikking stelt.

Als smaakmaker vind je in bijlage vijf werkbladen over statistiek uit het nummer 18/1 van december 2001.

Met dank aan de redactie!

Bijlagen:
Werkblad1_komkommertijd.pdf (3.9 KB)   
Werkblad2_normale_dichtheidsfuncties_en_de_standaardnormale_dichtheidsfunctie.pdf (19.6 KB)   
Werkblad3_examenresultaten_vergelijken.pdf (24.5 KB)   
Werkblad4_ben_ik_groter_dan_mijn_grootvader.pdf (4.4 KB)   
Werkblad5_dozen_erwten_vullen.pdf (24.6 KB)   

WISKUNDE EN MUZIEK

De Guidonische lettergrepen zijn de oud-Latijnse benamingen van de zes tonen van het hexachord, ut-re-mi-fa-sol-la, een groep van zes opeenvolgende tonen.

De zes benamingen werden in de 11e eeuw bedacht door Guido van Arezzo.

Pas in de 19e eeuw werd er een zevende toon aan het stelsel toegevoegd en in sommige landen de ut vervangen door do.

De Guidonische lettergrepen  werden in de Middeleeuwen gebruikt om zangers direct van het blad te leren zingen, zonder voorstudie van het materiaal.

De namen werden ontleend aan de - in die dagen overbekende - hymne Ut quaeant laxis, een hymne van Paolo Diacono (Paolo di Varnefrido (720-799)) ter ere van Johannes De Doper.

In de Latijnse tekst hieronder herken je ongetwijfeld de noten ut-re-mi-fa-sol-la-si als beginwoord of beginletters van de woorden:

Het octaaf is in de muziek het interval tussen twee tonen waarvoor geldt dat de frequentie van de ene toon precies het dubbele is van die van de andere.

In dat verband wordt de toon met de dubbele frequentie wel het octaaf van de andere toon genoemd.

Het woord octaaf is afgeleid van het Latijnse octavus, dat "achtste" betekent.

Een diatonische toonladder (dat is de basistoonladder van de westerse muziek) bestaat namelijk uit acht noten, en beslaat precies een octaaf,

dat wil zeggen dat de eerste en de achtste noot precies een factor twee in toonhoogte verschillen. 

Bron: Wikipedia.

Hieronder staat een octaafafstand tussen twee tonen C aangeduid op een pianoklavier.



Sinds het begin van de 19de eeuw worden piano's meestal gestemd volgens de zogenaamde evenredige twaalftoonstemming.

Dit betekent dat men het octaaf indeelt in 12 intervallen.

Wanneer men vertrekt van een toon met frequentie ν (bv. de la, die volgens internationale afspraak overeenkomt met een toon van 440 Hz),

bekomt men zo een meetkundige rij van 13 deelpunten of 12 intervallen met frequenties ν, kν, k²ν, k³ν, ..., k¹¹ν, k¹²ν. 

Dit komt overeen met een octaaf en dan volgt hieruit dat k¹²ν = 2ν  (nl. verdubbeling van de frequentie).

Dit betekent dat de factor k gelijk is aan 2^1/12 (de twaalfdemachtswortel van 2 = ¹² √2 ).

Volgens de sensatiewet van Fechner ervaren we deze prikkels (die een meetkundige rij met reden 2^1/12 vormen) als opeenvolgende termen van een rekenkundige rij.

Die rij bekomt men door van de bovenstaande meetkundige rij de ²log te nemen:  ²log ν, 1/12 + ²log ν, 2/12 + ²log ν, ..., 11/12 + ²log ν, 1 + ²log ν.

Merk op dat dit een rekenkundige rij is met verschil  ²log 2^1/12 = 1/12.

Een mooie toepassing van de meetkundige rij met reden 2^1/12 vindt men in de afstanden tussen de zogenaamde frets (ijzeren staafjes op de hals) van een gitaar. 

Als we de afstand van de kam tot een bepaalde fret aanduiden met d_i en de afstand van de kam tot de daaronder liggende fret met d_i+1, dan is de d_i /d_i+1 = 2^1/12.


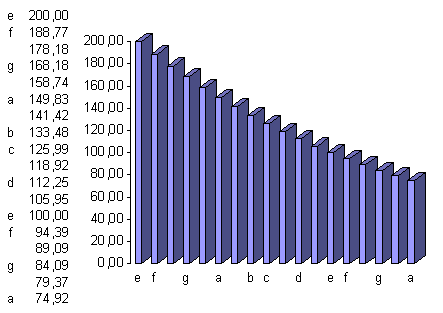
Dezelfde regelmaat vindt men ook terug bij orgelpijpen. Hieronder zie je hiervan een visuele voorstelling.

De langste pijp meet bv. 200 cm en door telkens de lengte van een pijp te delen door ¹² √2 krijg je lengte van de volgende pijp. Bron: www.wisfaq.nl.



Je vindt hierbij nog drie bijlagen.

Rijen 1. Een tekst van UHasselt in het kader van 'Geboeid door Wiskunde en Wetenschappen'.
Deze tekst behandelt o.a. de rij van Fibonacci, rekenkundige en meetkundige rijen, fractalen (driehoek van Sierpinski en sneeuwvlok van Koch).

Rijen 2. Een bewerking van de vorige tekst door collega Leon Lenders (Bree). Hierbij zit een originele bijdrage over 'een harmonische stapel bakstenen'.

Rijen en frets op een gitaar, door Martijn de Bruijn en Ramon Handulle (Technische Universiteit Delft).

Voor wie meer wil weten over de plaatsing van de frets op een elektrische of een akoestische gitaar.

Bijlagen:
Rijen1.pdf (294.7 KB)   
Rijen2.pdf (141.3 KB)   
Rijen_en_frets_op_een_gitaar.pdf (84 KB)