EEN EENVOUDIG MEETKUNDEPROBLEEM

Hoe teken je een driehoek met dezelfde oppervlakte als een gegeven (convexe) vierhoek?

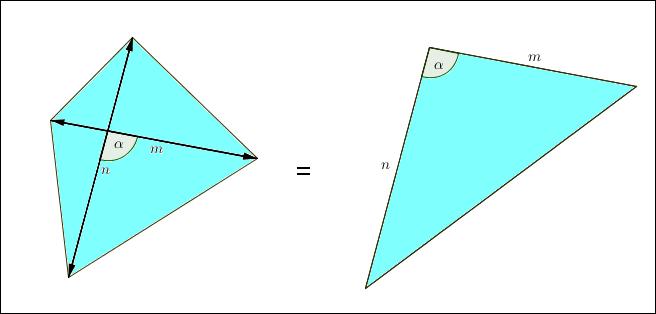
Op de bovenstaande figuur staat een verrassend eenvoudige oplossing afgebeeld.

De diagonalen van de vierhoek hebben lengte m en n en vormen een hoek α.

Kan je aantonen dat de oppervlakte van deze vierhoek gelijk is aan ½ mn sin α ?

Dit is dan uiteraard gelijk aan de oppervlakte van de afgebeelde driehoek!

HINT. De vier hoeken om het snijpunt van de diagonalen hebben dezelfde sinuswaarde.

EEN EENVOUDIG GETALLENPROBLEEM

2 x 3  + 3 x 4  –  1 x 4  –  2 x 5 = 4

3 x 4  + 4 x 5  –  2 x 5  –  3 x 6  = 4

4 x 5 + 5 x 6  –  3 x 6  –  4 x 7  = 4

5 x 6 + 6 x 7  –  4 x 7  –  5 x 8 = 4

...

Kan je bewijzen dat dit zo eindeloos verder gaat?

.

28-06-2015 om 09:16 geschreven door Luc Gheysens  

Rhodos 2015 - Luc Janus

***********************************************************************************************************

403 x 5 = 2015

403 = 13 x 31

int(e⁶) = 403

403 = 202² – 201²

403 = 3² + 13² + 15²

403 is een heptagonaal getal (zevenhoeksgetal)

ἓν οἶδα ὅτι οὐδὲν οἶδα

Eén ding weet ik zeker: dat ik niets weet.  (Sokrates)

Δεν ελπίζω τίποτα. Δε φοβούμαι τίποτα. Είμαι λέφτερος.

Ik hoop niets. Ik vrees niets. Ik ben vrij.  (Nikos Kazantzakis)

27-06-2015 om 00:00 geschreven door Luc Gheysens  

POLYGONE RING



Onder een polygone ring versta ik het vlak gebied
ingesloten tussen twee concentrische regelmatige veelhoeken
zoals op de bovenstaande figuur.

De oppervlakte A van een dergelijke ring met breedte h begrensd door twee regelmatige n-hoeken met zijden z en Z
is uiteraard gelijk aan de som van de oppervlakten van n trapeziums en is bijgevolg gelijk aan

en dit is precies de halve breedte h van de ring vermenigvuldigd met de som van de omtrekken van beide veelhoeken.

OPGAVE

25-06-2015 om 15:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*******************************************************************************
35

Wrong sum - Luc Janus

Zelfs Philippe Muyters, voormalig Vlaams minister van Financiën en Begroting wist dat 35 + 72 = 117.

*********************************************************************************

35 is een viervlaksgetal (1 + 3 + 6 + 10 + 15 = 35)

*********************************************************************************

Er zijn 35 verschillende hexomino's.

Weet jij hoeveel van deze figuren tot een kubus kunnen gevouwen worden? 

22-06-2015 om 00:00 geschreven door Luc Gheysens