|

De Grieken kenden reeds een constructiemethode om met behulp van een passer en een liniaal een willekeurige hoek in twee gelijke hoekjes te verdelen.
Ongetwijfeld heb jij deze constructie zelf nog uitgevoerd. Hieronder zie je hoe dit in zijn werk gaat.

De trisectie (of het in drie gelijke
hoekjes verdelen) van een willekeurige hoek bleek een onoplosbaar probleem te
zijn.
Ondertussen heeft men bewezen dat dit in het algemeen met behulp van een passer
en een liniaal niet mogelijk is.
Creatieve wiskundigen hebben echter in de 19de eeuw een soort 'tomahawk'
ontworpen
waarmee men de trisectie toch in het algemeen kan uitvoeren.
Hieronder staat zo een tomahawk
afgebeeld (lichtblauwe figuur - bron: http://mathworld.wolfram.com/Tomahawk.html ) .
Dit toestelletje kan je zelf maken in karton.
Rechts bemerk je een halve cirkelschijf met middelpunt T en diameter [SU].
Het lijnstuk [RU] is in drie gelijke delen verdeeld : |RS| = |ST| = |TU|. Let er ook op dat [SV] een
recht lijnstuk is.
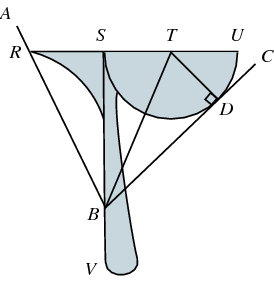
Hoe kan je nu hiermee de hoek met hoekpunt B en benen [BA en [BC in drie gelijke delen verdelen?
1. Plaats de tomahawk zo op de figuur dat het hoekpunt B op het lijnstuk [SV] ligt.
2. Zorg ervoor dat het punt R op het been [BA ligt.
3. Zorg ervoor dat het been [BC raakt aan de halve cirkel die een onderdeel is van tomahawk.
Je kunt dan gemakkelijk nagaan dat Δ BSR , Δ BST en Δ BDT congruente rechthoekige driehoeken zijn.
Hieruit volgt dan meteen dat de drie hoekjes met hoekpunt B even groot zijn!

10-09-2011 om 00:00
geschreven door Luc Gheysens 
|
