In zijn Liber Assumptorum bestudeert Archimedes twee merkwaardige figuren
die zijn opgebouwd met behulp van halve cirkels:
de salinon (Grieks voor zoutschaaltje) en
de arbelos (Grieks voor schoenmakersmes).



              
                                                                 salinon                                           arbelos                                                  

Een salinon is opgebouwd met behulp van 4 halve cirkels en heeft een verticale symmetrieas.
Een arbelos is opgebouwd met behulp van 3 halve cirkels.

Archimedes bewees:

 1. De oppervlakte van de salinon is gelijk aan de oppervlakte van de cirkel
met als diameter het lijnstuk
dat het hoogste en het laagste punt van de salinon verbindt.



2. De oppervlakte van de arbelos is gelijk aan de oppervlakte van de cirkel
met als diameter het lijnstuk [CD]
zoals aangeduid op de onderstaande figuur
(C is het punt waar de twee kleinere cirkelbogen elkaar ontmoeten,
D ligt op de grootste cirkelboog en CD staat loodrecht op AB).




Merk op: een arbelos met een verticale symmetrieas
is een bijzonder geval van een salinon.

Graag merken we ook nog de volgende eigenschap op:
de totale omtrek van de arbelos hangt niet af van de ligging van C op het lijnstuk  [AB].

Kan je de drie vermelde eigenschappen ook bewijzen?

Oplossing in bijlage.
Graag zelf eerst even zoeken a.u.b.

Bijlagen:
SALINON en ARBELOS.pdf (207.9 KB)   

Als wiskundige ben je soms verbaasd over heel eenvoudige patronen die opduiken bij het maken van bewerkingen.

Rariteit 1



0 x 1 x 2 + 1 = 1 = 1³
1 x 2 x 3 + 2 = 8 = 2³
2 x 3 x 4 + 3 = 27 = 3³
3 x 4 x 5 + 4 = 64 = 4³
enzovoort ...

Kan je dit in het algemeen bewijzen?


Rariteit 2



1 + 3 = 4 x 1
1 + 3 + 5 + 7 = 4 x (1 + 3)
1 + 3 + 5 + 7 + 9 + 11 = 4 x (1 + 3 + 5)
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 4 x (1 + 3 + 5 + 7)
enzovoort ...

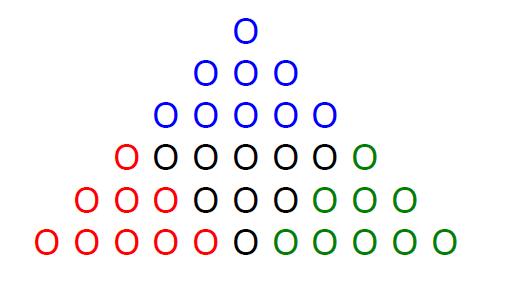
Kan je op de onderstaande figuur 'zien' dat  1 + 3 + 5 + 7 + 9 + 11 = 4 x (1 + 3 + 5) ? 

13-04-2012 om 00:00 geschreven door Luc Gheysens  

RAADSEL

Sigiswald wil drie stoelen (gelijk geprijsd), een tafeltje en een spiegel kopen.
Hij ziet het setje van zijn dromen staan in de WEBA,
maar helaas heeft hij niet genoeg geld bij zich om de 5 artikelen samen te kopen.
Hij kan wel 4 van de 5 artikelen kopen.
Afhankelijk van zijn keuze kosten 4 artikelen 1264, 1364 of 1800 euro.
Dat kan hij allemaal betalen.

Hoeveel euro kosten de vijf artikelen samen?

Het antwoord en nog veel meer leuke raadsels vind je op http://www.debacker.info/raadsels.asp .
Hieronder kan je meteen nog meegenieten van mijn favoriete WEBA-promotieclip.

13-04-2012 om 00:00 geschreven door Luc Gheysens