|
PARABOLEN GEVEN HUN GEHEIM PRIJS
Hoe kan je op de grafiek van een parabool met als functievoorschrift y = f(x) = ax² + bx + c
de waarde van de coëfficiënten a, b en c aflezen?
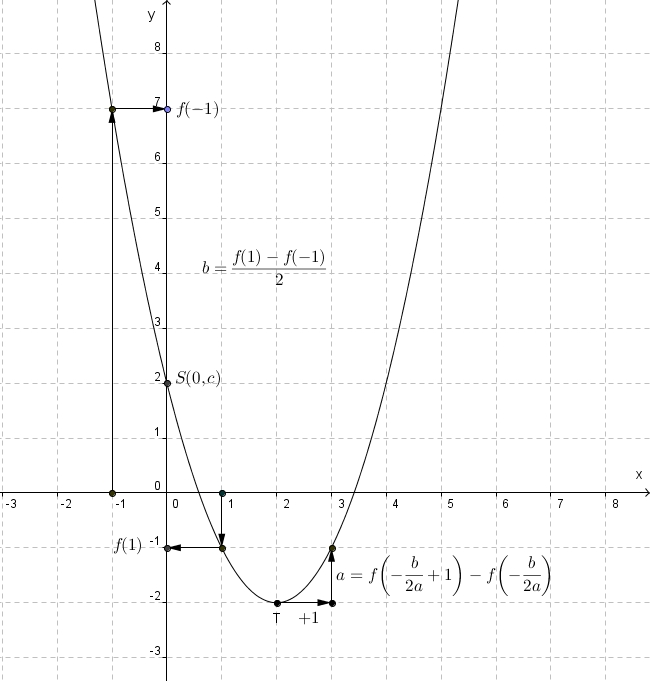
1. Voor de waarde van a : ga vanuit de top T één eenheid horizontaal naar rechts;
dan is a de relatieve verticale afstand vanuit dat punt tot aan de parabool.
a > 0 als je naar boven moet gaan en a < 0 als je naar beneden moet gaan.
In het bovenstaande voorbeeld is a = 1.
2. Voor de waarde van b bereken je (f(1) - f(-1))/2. In het voorbeeld is b = (-1 7)/2 = -4.
De waarde van b is eveneens de richtingscoëfficiënt van de raaklijn aan de parabool
in het snijpunt met de y-as, want f '(x) = 2ax + b en dus is f ' (0) = b.
3. De waarde van c is de y-coördinaat van het snijpunt S van de parabool met de y-as.
In het voorbeeld is c = 2.
Besluit: de afgebeelde parabool heeft als vergelijking y = x² 4x + 2.

En misschien kunnen de vier opgaven in bijlage jouw enthousiasme voor parabolen nog doen toenemen?
Bijlagen:
Vier parabolen.pdf (126.2 KB)
11-04-2015 om 00:00
geschreven door Luc Gheysens 
|
