PELLGETALLEN

De Pellgetallen zijn genoemd naar de Engelse wiskundige John Pell (17de eeuw)
en worden gedefinieerd door de volgende recursiebetrekking:

Deze rij begint dus met 0 en 1 en elk volgend getal bekomt men
door tweemaal het vorige getal op te tellen bij het getal daarvoor.
 
De rij begint dus als volgt:  0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2 378...

Het n-de Pellgetal is bepaald door de volgende uitdrukking:

Bron: Wikipedia.



In de bijlage kan je zien hoe je de bovenstaande uitdrukking
voor het n-de Pellgetal kunt vinden.

En op de onderstaande figuur hebben we geprobeerd de rij van de Pellgetallen te 'visualiseren'.

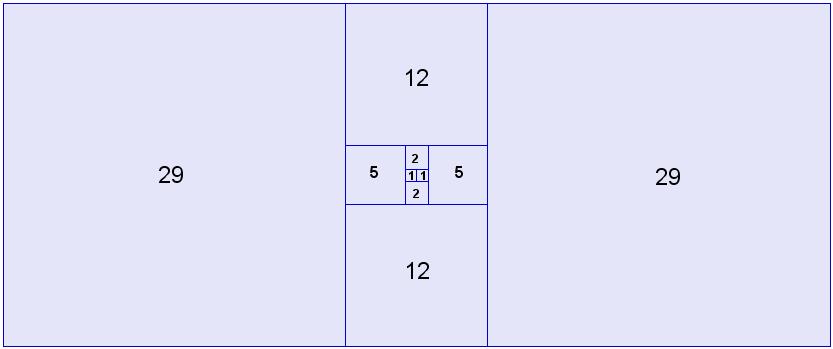
Lees ook eens de bijlage waaruit blijkt dat men zowel de Fibonaccigetallen als de Pellegetallen met een grafische rekenmachine kan genereren.

Bijlagen:
Algemene uitdrukking van de Pellgetallen.pdf (214.9 KB)   
FIBONACCI EN PELLGETALLEN.pdf (204.6 KB)   

Om een stelsel van n lineaire vergelijkingen op te lossen
waarbij de determinant van de coëfficiëntenmatrix verschillend is van nul
bestaat er een elegante oplossingsmethode die gebruik maakt van determinanten:

DE REGEL VAN CRAMER

die we hieronder vermelden voor een 3 x 3 - stelsel.

Gabriel Cramer (1704 - 1752) was een Zwitserse wiskundeprof die werkte aan de Universiteit van Genève.
In 1750 publiceerde hij een boek over algebraïsche krommen
waarin hij o.a. bewees dat een vlakke kromme van de n-de graad
in het algemeen bepaald is door n(n+3)/2 punten.
Zo is bijvoorbeeld een kegelsnede (tweedegraadskromme) bepaald door 5 punten. 

In de bijlage bij dit werk publiceert hij een methode om stelsel op te lossen, die nu bekend staat als de regel van Cramer.
Hiermee gaf hij een aanzet tot de ontwikkeling van de theorie van determinanten.

Een kort bewijs van deze regel vind je in de bijlage.

Bijlagen:
De regel van Cramer - bewijs.pdf (177.8 KB)   

 

PROBLEEM 8

UITVINDING 8

Deze snelle driewieler was een uitvinding van een zekere
Mr. Vossner uit Philadelphia.
Hij bedacht een ingenieus systeem om de beweging van de pedalen
over te brengen op de grote wielen van deze fiets.
Eén toer met de pedalen resulteerde in twee volledige toeren van de wielen
zodat men terecht kon spreken van een snelle driewieler.

Bijlagen:
COSMOSPROBLEEM 8_oplossing.pdf (216.1 KB)   

EEN MERKWAARDIGE SOM

Een bewijs zonder woorden zie je hieronder!

Bron: Mathematics Magazine, Vol. 62, No. 5 

***********************************************************************************************

Collega Daniël Tant bezorgde me een bewijs 'met woorden':

27-03-2014 om 00:00 geschreven door Luc Gheysens  

SOM VAN EEN MEETKUNDIGE REEKS

Een gelijkbenig trapezium kan je opdelen in vier congruente gelijkbenige trapeziums

en hiermee bewijs je 'zonder woorden ' dat

1/4 + 1/16 + 1/64 + ...  = 1/3.

Dit is een bijzonder geval van een algemene formule voor de som van een meetkundige reeks.

Hieronder zie je een bewijs zonder woorden voor deze algemenere formule.

Gezien?

26-03-2014 om 00:00 geschreven door Luc Gheysens  

STANGENVLINDERS

Een constructie bestaat uit twee stangen van lengte 18 cm en twee stangen van lengte 10 cm,
die scharnierend aan elkaar bevestigd zijn. We verwaarlozen de breedte en de dikte van de staven.
Wanneer de stangen scharnieren rond de punten A, B, C en D ontstaan figuren
die we stangenvlinders noemen. Hieronder staan er een paar  getekend.

De afstand tussen A en B is x en de afstand tussen C en D is y.
Druk het verband uit tussen x en y.

Oplossing in bijlage.
Bron: Tijdschrift voor Didactiek der β-wetenschappen, Jaargang 28 nr. 1 (2011)

Bijlagen:
Stangenvlinders - rekenwerk.pdf (145.7 KB)   

HET PROBLEEM VAN DE VIER LUIZEN

Vier luizen zitten op de vier hoekpunten van een vierkant met zijde 1.
Elke luis loopt in tegenwijzerzin in de richting van de luis rechts ervan
(die dus zelf ook aan de loop gaat) en we nemen aan
dat de luizen met dezelfde snelheid naar elkaar toe lopen.

Het zal wel duidelijk zijn dat de vier luizen elkaar in het midden van het vierkant ontmoeten.
Maar welk traject hebben ze dan afgelegd en hoe lang is dat traject?  

In de bijlage tonen we aan dat ze lopen volgens een logaritmische spiraal. Puur wiskundig bekenen zouden de vier punten oneindig lang naar elkaar toe bewegen en paradoxaal genoeg is 'de totale afstand' die elke luis aflegt gelijk aan 1 wat precies de lengte van de zijden van het vierkant is.

HET PROBLEEM VAN DE DRIE LUIZEN.

Welke afstand zouden drie luizen afleggen
als ze starten op de hoekpunten van een gelijkzijdige driehoek
waarvan de zijden lengte 1 hebben?

Wiskundigen zijn erin geslaagd een elegante formule te vinden
voor de afgelegde afstand d_n wanneer de luizen starten
op de hoekpunten van een regelmatige n-hoek met zijden 1:

Meer uitleg op http://www.cut-the-knot.org/Curriculum/Geometry/FourTurtles.shtml 
De baan die ze volgen is dan telkens een logaritmische spiraal.

Bron: Wolfram Mathworld.

Bijlagen:
HET PROBLEEM VAN DE VIER LUIZEN.doc (198 KB)