|
1, 4, 9, 16, 25, ... is de rij van de kwadraatgetallen (kwadraten van de gehele getallen).
Maar wist je dat ...

42 = 24 = 16 en hiermee is 16 wellicht het merkwaardigste kwadraatgetal.

4 1 = 3 en 9 4 = 5 en 16 9 = 7 en 25 16 = 9 ...
Het verschil tussen twee opeenvolgende kwadraatgetallen is dus steeds een oneven getal.
Bovendien is elk oneven natuurlijk getal groter dan of gelijk aan 3 het verschil van twee kwadraatgetallen: 2n + 1 = (n + 1)² n².

Bekijk de rij 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8.
Hierin staan alle gehele getallen van 1 tot en met 16 zodanig gerangschikt dat de som van elke twee opeenvolgende getallen een kwadraatgetal is: 16 + 9 = 5², 9 + 7 = 4², 7 + 2 = 3² enzovoort ...

1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15
16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24
en zo kan je eindeloos doorgaan ...
Merk op dat elke lijn begint met een kwadraatgetal (1, 4, 9, 16 ...).

En ook het getal pi ontsnapt niet aan de kwadraatgetallen (formule van Euler):
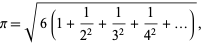

29-08-2011 om 00:00
geschreven door Luc Gheysens 
|
