Een cycloïde is de kromme die wordt gedefinieerd door de baan van een punt op de rand van een cirkelvormig wiel 
als die cirkel over een rechte lijn rolt (zonder glijden).

Als de cirkel een straal r heeft, bekomt men als parametervergelijkingen van de cycloïde (zie bijlage):

x = r(t - sint)
y = r(1 - cos t).

De parameter t geeft aan over welke hoek de cirkel vooruitrolt.

Bij één volledige omwenteling van de cirkel varieert t van 0 tot 2π.
De lengte van één boog van een cycloïde is gelijk aan 8r (zie bijlage). 




In de 17de eeuw zochten wiskundigen naar de kromme die een bijzonder soort 'glijbaan' beschreef.
Men stelde zich immers de vraag of er een helling bestond
met de eigenschap dat als men er ballen vanop verschillende startposities tegelijk op liet naar beneden rollen,
die ballen dan ook tegelijk aan de voet van de helling zouden aankomen
ongeacht de positie van waarop men ze losliet.

De Nederlandse wis-, sterrenkundige en natuurkundige Christiaan Huyghens
ontdekte in 1659 dat die helling werd beschreven door een 'omgekeerde' cycloïde
 (zie onderstaand applet - bron wikipedia).

Huyghens wou deze ontdekking gebruiken om een nauwkeuriger slingeruurwerk te ontwerpen
en publiceerde zijn ontdekking in 1673 in zijn 'Horologium Oscillatorium' ( =  'Het Slingeruurwerk').




Wegens deze bijzondere eigenschap wordt deze kromme ook de tautochrone of isochrone kromme genoemd
(Grieks: τὸ αὐτό, dezelfde, ισος, gelijk en χρονος, tijd).

Deze kromme heeft  nog een andere merkwaardige eigenschap.
Ze beschrijft ook de helling waarlangs een voorwerp zonder wrijving
zich tussen twee punten verplaatst in de kortst mogelijke tijd.
Daarom spreekt men ook van de brachistochrone kromme
(Grieks: βραχιστος, kortste en χρονος, tijd).
Bron: wikipedia.

Collega Ferdinand Develter merkt terecht op dat deze kromme
die zorgt voor de snelste daling ook zorgt voor de traagste stijging.
Dit vindt o.a. zijn toepassing bij kaaimuren, de boeg van een schip ...

Bijlagen:
Studie van de cycloide.pdf (95.1 KB)   

Newton realiseerde zich dat de maan
in feite elke seconde en beetje naar de aarde toe valt
precies op dezelfde manier als een appel
van een boom naar de aarde valt.

Als dit niet zo was
dan zou de maan immers in een rechte lijn
met een constante snelheid
door de ruimte van de aarde wegvliegen.

De kracht die de maan in haar (min of meer) cirkelvormige baan houdt
noemde hij de centripetale kracht.

We rekenen eens uit hoeveel de maan per seconde naar de aarde toe valt.

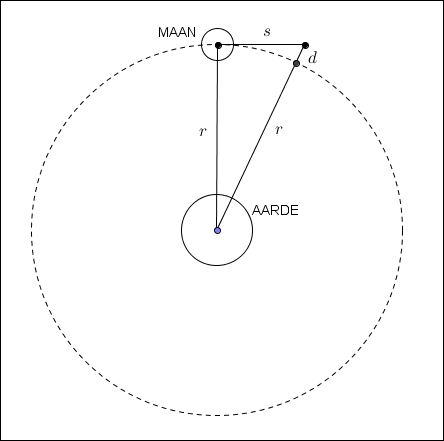
Op deze figuur is
r = de gemiddelde afstand van de maan tot de aarde, ongeveer 386 000 km
s = de afstand door de maan afgelegd van de aarde weg in 1 seconde
d = de afstand die de maan naar de aarde toe valt in 1 seconde.

Wegens de stelling van Pythagoras is  r² + s² = (r + d)² of r² + s² = r² + 2rd + d², zodat s² = 2rd + d².

Hierbij is d vrij klein, zodat we het nog veel kleinere d² kunnen verwaarlozen. Dus is d = s²/(2r) .      (1)

s is ook heel klein zodat we deze afstand mogen benaderen door de lengte van de cirkelboog die de maan in 1 seconde aflegt, d.w.z.

Met r = 386 000 000 (in meter) vinden we hieruit dat s = 2π x 386 000 000 x 4,1 x 10^-7 = 1002,5 meter. 

Door tenslotte deze waarde in te vullen in (1) vinden we dat d = 0,0013 meter.

Dit betekent dat de maan elke seconde ongeveer 1,3 millimeter naar de aarde toe valt
en zo op een min of meer cirkelvormige baan rond de aarde kan blijven rondtoeren. 

MAANSVERDUISTERING

Morgenavond woensdag 15 juni 2011 is het voor heel wat amateur-astronomen weer een hoogdag,
want dan vindt er een totale maansverduistering plaats.

De maansverduistering start woensdag om 20.23 uur.

Het hemellichaam zit dan echter nog onder de horizon, waardoor de eclips dus nog niet waargenomen kan worden.
Anderhalf uur later, om 21.53 uur, komt de maan op in het zuidoosten van de hemel. Ze is dan al volledig verduisterd.
Om 22.13 uur is de maansverduistering totaal.
Die totale eclips eindigt om 23.03 uur.
Om 24 uur zou de maan opnieuw volledig te zien zijn.  

De amateurs van leuke powerpointpresentaties moeten maar eens de bijlage openen
om zo mee te genieten van 'spelen met de maan'.

Bijlagen:
Playing with the moon.pps (2.2 MB)   

Flatland: A Romance of Many Dimensions (Nederlands: Platland: een roman van vele afmetingen) is in 1884 geschreven door Edwin Abbott Abbott, een Engelse schoolmeester en theoloog. Hij probeert de lezer op informele wijze de mogelijkheid (de wiskundige waarschijnlijkheid zelfs) van meerdere dimensies uit te leggen.

Flatland volgt de avonturen van A. Square (Nederlands: Een Vierkant) die op een dag wordt bezocht door een cirkel (die eigenlijk een bol blijkt te zijn die als cirkel verschijnt in Flatland) en die hem uit z'n tweedimensionale wereld tilt en hem meeneemt naar lijnland en puntland om hem duidelijk te maken dat er meer dimensies zijn dan alleen de 2 van Flatland. Als A. Square aan de bol vraagt of er misschien zelfs meer bestaan dan de 3 waar de bol vandaan komt, wordt deze boos en stopt hem weer terug in zijn tweedimensionale wereld.

Dit boekje laat ons meteen nadenken over de mogelijkheid dat er meerdere dimensies bestaan, dan we werkelijk waarnemen. In bijlage vind je de Nederlandse vertaling van Flatland.

Flatland: The Movie is een leuke animatiefilm uit 2007 waardoor het werk van Edwin A. Abbott weer in de belangstelling is gekomen. Hieronder kan je de officiële trailer van deze film bekijken.

Onwillekeurig denk je hierbij ook aan de allegorie van de grot uit de kennisleer van Plato (uit zijn werk Politeia). Hierin beschrijft hij hoe een aantal mensen sedert hun geboorte gevangen zitten in een grot. Tegen de wand van de grot zien de schaduwen geprojecteerd van werkelijke objecten, maar de realiteit zelf kennen en begrijpen ze niet.

Einstein leerde ons al dat we leven in een vierdimensionale tijd-ruimte met de klassieke drie dimensies (lengte, breedte en hoogte) en de tijd als vierde dimensie. De snaartheorie (string theory) gaat er echter van uit dat we leven in een ruimte met misschien wel 10 of 11 dimensies. Onze gezichtsorganen zijn echter onvoldoende ontwikkeld om de immens kleine deeltjes, die ontstaan als trillingen van een snaar, waar te nemen.

Om dit te begrijpen verwijst men vaak naar het beeld van een tuinslang. Als we die vanop een afstand bekijken, hebben we de indruk dat een tuinslang een tweedimensionaal voorwerp is (met een lengte en een kleine breedte), maar voor een mier die erover kruipt is een tuinslang een driedimensionaal voorwerp!

Dimensies staan duidelijk weer in de belangstelling. Dat bleek onlangs nog op de proclamatie van de Vlaamse Wiskunde Olympiade, waarbij de Franse wiskundige Etienne Ghys (Ecole Normale Supérieure, Lyon) o.a. de bekroonde film 'Dimensions' kwam voorstellen. Je kunt de 9 hoofdstukken van deze fascinerende film gratis bekijken op http://www.dimensions-math.org/Dim_NL.htm . Vooral hoofdstuk 2 (over de derde dimensie) en hoofdstuk 3 (over de vierde dimensie) zijn warm aanbevolen.

Bijlagen:
platland.pdf (976.5 KB)   

Drie missionarissen en drie kannibalen moeten met behulp van een bootje naar de overkant van een rivier worden gebracht.

In het bootje kunnen echter hoogstens twee personen tegelijk plaatsnemen

en nooit mogen er meer kannibalen dan missionarissen op een oever achterblijven,

want anders beginnen de kannibalen vlot aan hun lunch ...

Hoe krijg je dit voor elkaar?

Je kunt dit spelletje online spelen op http://www.plastelina.net/game2.html .

Voor wie er toch niet aan uit geraakt, hebben we een oplossing in bijlage gestopt.

Maar ... zeker eerst zelf blijven zoeken!

 

Bijlagen:
3 missionarissen en 3 kannibalen.doc (22 KB)   

 

1. Hoeveel letters 'F' tel je in de volgende tekst?

FINISHED FILES ARE THE
RESULT OF YEARS OF SCIENTIFIC STUDY
COMBINED WITH
THE EXPERIENCE OF YEARS...


2. Wat lees je hieronder?

Alelen silmme msenen knunen dit lzeen.
Ik kon het neit glevoen teon ik het zag. 
De fnemoeanl pwoer van je hrenesen 
palatst alles in de jiutse vlogodre.
Vloegns een sutide van de Unvireitsiet van Cmabrigde,
makat de vlogodre van de ltretes in een wrood neits uit ,
je meot alelen zrgoen dat je de ereste en de latsate lteter
op jiuste plek zet. Van de rset mag je een zioojte mkaen.
Dat kmot odmat je hrenesen neit lteetr per leettr leezn,
maar wel de gorep lteters bij eklaar.


3. Wie goede ogen heeft, kan de onderstaande tekst wellicht direct lezen...

*******************************************************************************

Oplossingen.

1. Er staan 6 letters 'F'. Tel nog eens na ...
3. In het wit staat: NO SEX CAUSES BAD EYES.

Bron: http://www.planetperplex.com

13-06-2011 om 00:00 geschreven door Luc Gheysens