|
INHOUD VAN EEN PRISMOÏDE
Een prismoïde is een convex veelvlak (ruimtelijke figuur)
waarvan de hoekpunten in twee evenwijdige vlakken (grondvlak en bovenvlak) liggen.
De afstand tussen de twee evenwijdige vlakken noemt men de hoogte van de prismoïde.
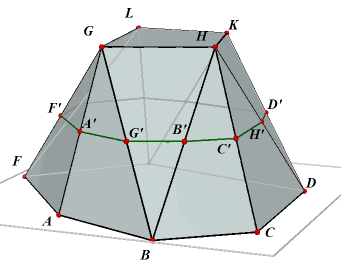
Hieronder staat ëen prismoïde afgebeeld waarbij ook het middenvlak is getekend.
In een Egyptische papyrus die dateert van ongeveer 1890 v. Chr.
duikt voor het eerst een merkwaardige formule op voor het volume V van een prismoïde:
G = oppervlakte grondvlak, M = oppervlakte middenvlak, B = oppervlakte bovenvlak, h = hoogte.
Het was de Engelse wiskundige Thomas Simpson die in 1743 de formule in het algemeen bewees m.b.v. een bepaalde integraal.
Hiermee veralgemeende Simpson zijn gekende formule uit de numerieke integratie
om de oppervlakte van een vlak gebied bij benadering te berekenen:
![int_{a}^{b} f(x) , dx approx frac{b-a}{6}left[f(a) + 4fleft(frac{a+b}{2}right)+f(b)right].](http://upload.wikimedia.org/math/c/d/1/cd18b1d075e9c7d4e65314c8e95ccb45.png)
Uitleg over de prismoïde vind je o.a. op http://www.pandd.nl/stereo/prismoide.htm
In de bijlage 'reconstrueren' we de formule van Simpson voor de inhoud van een prismoïde.
Bijlagen:
FORMULE VAN SIMPSON VOOR DE INHOUD VAN EEN PRISMOÃDE.pdf (174.5 KB)
18-04-2014 om 00:00
geschreven door Luc Gheysens 
|
Kan je deze vondst van Archimedes bewijzen in een bijzonder geval (zie bijlage).
