Le Théorème du Petit Prince

De opgave van vandaag komt van een Kleine Prins vanop zijn asteroïde B 612.

Oplossing in bijlage.

******************************************************************************************************

Is de naam B 612 van de asteroïde vanwaar de Kleine Prins afkomstig is een geheime code?

Misschien verstopte Antoine de Saint-Exupéry hierin de volgende boodschap:
de 6de, 1ste en 2de letter van het alfabet vormen het drieletterwoord FAB (afkorting van 'fabulous') en B leest men als 'be'.
De boodschap luidt dan: BE FABULOUS of probeer op jouw manier 'fantastisch' te zijn.

En de FAB FOUR verklappen je ook nog graag eens hun geheimpje.

Bijlagen:
Le Théorème du Petit Prince.pdf (272.3 KB)   

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

1933

Le Coq sur Mer - Luc Janus

In 1933 verbleef Albert Einstein ongeveer drie maanden in De Haan aan zee.
Hij was er in feite op de vlucht voor het naziregime in afwachting dat hij naar Amerika kon oversteken.

********************************************************************************************************************

Op 2 augustus 1933 ontmoette hij er in het restaurant 'Le coeur volant'
de Vlaamse schilder James Ensor, de Franse minister van Onderwijs Anatole de Monzie en een plaatselijke schoonheid.

Bijlagen:
Einstein in De Haan.pdf (87.2 KB)   

PI-RING

In een scherphoekige driehoek met basis b = 6 en hoogte h = 3 tekent men een zo groot mogelijk vierkant (zie figuur).

De ring bepaald door de omgeschreven en de ingeschreven cirkel van dit vierkant heeft als oppervlakte π.

Bewijs dit!

Applaus voor wie de oplossing vindt (en alle anderen verwijs ik door naar de bijlage).

Bijlagen:
PI-RING - oplossing.pdf (333.6 KB)   

DE BROEK VAN JANNEKE DE REUS

Wie houdt van extremumvraagstukken kan eens proberen het onderstaande probleem op te lossen.

In een carnavalsoptocht stapt de reus Janneke mee op.

Het feestcomité wil dit jaar voor hem een nieuwe broek op maat laten maken.

Hieronder staat het patroon van het voorpand afgebeeld.

De broek moet 1 meter lang zijn en de opening van de beide broekspijpen 1 dm breed.

De kleermaker laat weten dat hij hiervoor een rechthoekig stuk stof zal gebruiken.

Voor de beenopening zal hij hieruit twee vierkanten met zijde x en een driehoek wegknippen.

De totale oppervlakte van het voorpand (na het wegknippen) bedraagt nog 56 dm².

GEVRAAGD.

1. Stel een formule op voor de lengte b van de broekspijpen in functie van x.

2. Voor welke waarde van x hebben de broekspijpen een maximale lengte?

3. Hoe lang zijn de broekspijpen dan?  

Gelukt?

De oplossing zit ook in bijlage.

Bijlagen:
DE BROEK VAN JANNEKE DE REUS - oplossing.pdf (172.4 KB)   

DOMINOSOMMEN

Bekijk eens het volgende sommenpatroon:

1= 1²

1 + 2  4 = 9 = 3²

1 + 2 4 + 2  8 = 25 = 5²

1 + 2 4 + 2  8 + 2  12 = 49 = 7²

                          1 + 2  4 = 3²                                                                             1 + 2  4 + 2  8 = 5²                       
  
Maar misschien maakt een muzikale Domino je vlugger enthousiast?

15-04-2015 om 00:00 geschreven door Luc Gheysens  

DE TUSSENBREUK

Deze eigenschap duikt voor het eerst op in het werk Le Triparty en la science des nombres
van de Franse wiskundige Nicolas Chuquet (15de eeuw).

Snap je het onderstaande 'bewijs zonder woorden'?

*************************************************************************************************

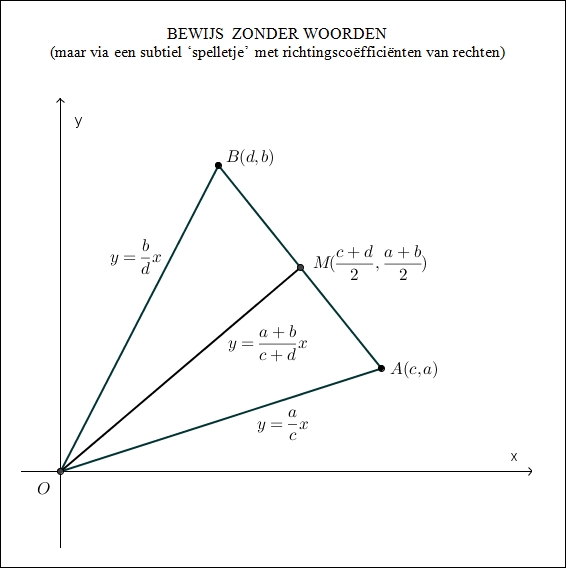
HISTORISCHE NOTA OVER NICOLAS CHUQUET

Deze Franse wiskundige leefde in de 15de eeuw en publiceerde een van de eerste boeken in de Franse taal over rekenkunde.
De invloed van zijn werk Le Triparty en la science des nombres wordt ruim onderschat.
Zoals de titel van het boek laat vermoeden, is het ingedeeld in drie hoofdstukken.

DEEL 1. Over gehele getallen en breuken. In dit deel legt hij o.a. de regel van drie uit.
Hij introduceert ook de termen biljoen en triljoen en stelt dus voor om het getal
745324' 804300' 700023' 654321 te lezen als 745324 triljoen 804300 biljoen 700023 miljoen en 654321.

DEEL 2. Over vierkantswortels. Hij legt hierin uit hoe je manueel de vierkantswortel uit een getal trekt.

DEEL 3. Over priemgetallen.

*******************************************************************************************

Wist je dat het getal pi een breuk is ?

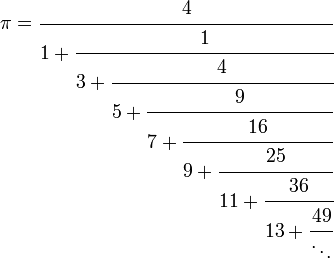
Maar dan wel een kettingbreuk...

14-04-2015 om 00:00 geschreven door Luc Gheysens  

A LA GRECQUE

Eeuwen geleden gingen de Griekse wiskundigen figuratief te werk.

Ze stelden dus algebraïsche eigenschappen en formules voor via meetkundige figuren.

Hieronder kan je op een bijna identieke figuur twee formules 'zien'.

EEN MERKWAARDIG VERSCHIL

(a + b)² – (a – b)² = 4ab

EEN EIGENSCHAP VAN DE FIBONACCIGETALLEN

De termen uit de van Fibonacci (1, 1, 2, 3, 5, 8, 13, 21 ...)  voldoen aan

F_n+1² – F_n-2² = 4 F_n F_n-1 .

Zo is bijvoorbeeld 13² – 3²  = 4 x 8 x 5  en 8² – 2² = 4 x 5 x 3.

13-04-2015 om 00:00 geschreven door Luc Gheysens