|
EEN STERK STAALTJE VAN PAPPOS - DEEL 1
Pappos van Alexandrië (ca. 290 - ca. 350 na Chr.)
was een van de laatste grote oud-Griekse wiskundigen.
Uit het werk dat hij ons heeft nagelaten, kunnen we opmaken
dat hij een sterk meetkundig inzicht had
en dat hij zich ook bezighield met recreatieve wiskunde.
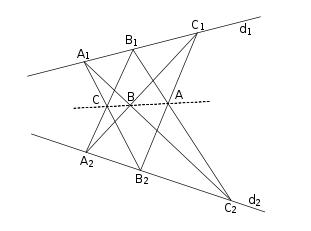
DE STELLING VAN PAPPOS
Liggen A1, B1 en C1 op een rechte d1 en liggen A2, B2 en C2 op een rechte d2 ,
dan zijn de volgende drie punten collineair:
A: het snijpunt van B1C2 en B2C1,
B: het snijpunt van A1C2 en A2C1,
en C: het snijpunt van A1B2 en A2B1.
Deze stelling werd later veralgemeend door Pascal voor een zeshoek ingeschreven in een kegelsnede.
Twee rechten vormen immers een zogenaamde ontaarde kegelsnede.
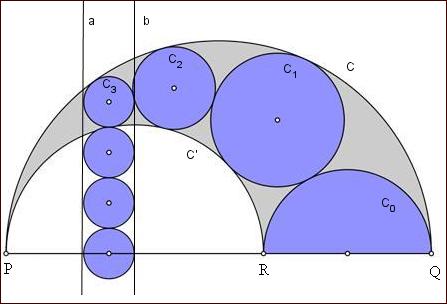
INGESCHREVEN CIRKELS IN EEN ARBELOS
In mijn middelbare studies was ik onder de indruk van de vondst van Pappos
in verband met cirkels die ingeschreven zijn in een arbelos (wat is dit?).
Deze merkwaardige ontdekking levert meteen een fraai plaatje op (zie hieronder).
Door gebruik te maken van een inversie (wat is dit?) met centrum P
worden de cirkels C0, C1, C2 en C3 die raken aan de (halve) cirkels C en C'
afgebeeld op een aantal even grote cirkels die raken aan de rechten a en b.
Ze raken ook aan elkaar omdat ook C0, C1, C2 en C3 aan elkaar raken.
Deze rechten zijn zelf het beeld onder de inversie van de cirkels C en C' en staan loodrecht op PQ.
Een inversie transformeert cirkels die het centrum van de inversie niet bevatten terug in cirkels.
De cirkel C3 wordt op zichzelf afgebeeld.
Pappos toonde bovendien aan dat het middelpunt van de cirkel Cn zich op een afstand n.dn
boven de rechte PQ bevindt, waarbij dn de diameter is van de cirkel Cn (n = 0, 1, 2, 3).

10-03-2014 om 00:00
geschreven door Luc Gheysens 
|
