PROBLEEM 6

UITVINDING 6

Dit toestel werd ontworpen om kostbaar fruit te plukken dat hoog in een boom hing.
Men plukte die meestal door er een tik tegen te geven
en ze daarna op te vangen in een soort kous.
Het fruit viel soms naast de kous of geraakte beschadigd bij het aantikken.
Het nieuwe ontwerp bestond uit een holle bamboestok
waarin twee metalen grijparmen waren gemonteerd
die men vanop de grond kon bedienen.

Bijlagen:
COSMOSPROBLEEM 6_oplossing.pdf (128.1 KB)   

INTEGREREN ZONDER MOEITE

Kan je verklaren waarom je de oplossing van de onderstaande drie bepaalde integralen

'op zicht' kunt vinden, zonder de onbepaalde integralen op te lossen?

Zag je direct dat er in beide integralen telkens twee functies voorkomen die elkaars inverse zijn?

Hieronder zie je hoe dit principe 'in het algemeen' werkt;

Gezien?

10-04-2014 om 00:00 geschreven door Luc Gheysens  

COMBINATIES

Het aantal manieren om 2 elementen te kiezen uit een verzameling van n elementen
noemt men het aantal combinaties van n elementen 2 aan 2
(of het aantal combinaties van 2 uit n).

Hiervoor geldt de volgende formule:

Een 'bewijs zonder woorden' zie je hieronder.

Voor wie toch een woordje uitleg wil:
op de onderste rij worden twee (donkerblauwe) ballen gekozen uit 7.
Met elke keuze van twee ballen uit deze rij 
blijkt precies één (oranje) bal overeen te komen uit de driehoek die daarboven is opgebouwd.
En die driehoek bevat 1 + 2 + ... + 6 ballen.

 

Geïnspireerd op: Wolfram Demonstrations Project

09-04-2014 om 00:00 geschreven door Luc Gheysens  

Zien is geloven

Eigenschap.

Als één van de scherpe hoeken van een rechthoekige driehoek een hoek van 15° is,
dan is de oppervlakte van deze driehoek één achtste van het kwadraat van de schuine zijde.

BEWIJS 1. Dit kan je gemakkelijk zelf vinden als je weet dat sin 15° cos 15° = ½ sin 30° = ¼.

BEWIJS 2. Je kan het bewijs 'zien' op de onderstaande figuur. Lukt dit?

09-04-2014 om 00:00 geschreven door Luc Gheysens  

In zijn rijkgevulde carrière van leraar wiskunde, eminente didacticus en vakbegeleider

met een fijne neus voor aantrekkelijke en bevattelijke onderwerpen heeft Walter heel wat mooie artikeltjes bijeengeschreven.

 Zijn bijdrage over 'Mieren op een kubus' is hiervan een schoolvoorbeeld dat heel wat collega's met gretigheid hebben verslonden (zie bijlage).

Het artikel 'Ode aan de wiskunde' was zijn laatste bijdrage in de functie van pedagogische begeleider wiskunde bij DPB-Brugge. 

Ook deze tekst, waarin probleemoplossend denken en ICT-gebruik - twee van Walters stokpaardjes - aan bod komen,  zit in bijlage.

Tenslotte vind je in bijlage nog een leuk artikel van de hand van Walter over de subnormaal bij een parabool. 

Walter wist heel wat studenten en collega's te inspireren en heeft de wereld van de wiskundigen te vroeg verlaten ...

Bijlagen:
DE SUBNORMAAL(Walter).pdf (123.7 KB)   
Mieren_op_een_kubus(Walter).pdf (110 KB)   
Ode aan de wiskunde (Walter).pdf (52.9 KB)   

De CHEBYSHEV-VEELTERMEN



In 1946 herdacht men de 125-ste verjaardag van de geboorte van de Russische wiskundige Chebyshev,
die belangrijke bijdragen leverde tot de statistiek, de kansrekening, de functieleer en de mechanica.

Hij is vooral gekend door de Chebyshev-ongelijkheid waarmee de wet van de grote aantallen wordt bewezen.
Die wet uit de kansrekening bewijst dat wanneer men een kansexperiment een heel groot aantal keer herhaalt,
de experimentele kans zal gelijk worden aan de theoretische kans.
Zo zal bv. bij 600 worpen met een dobbelsteen ongeveer 100 keer een zes worden gegooid
(terwijl men na 10 worpen nog geen enkele zes kan gegooid hebben).

Naar hem zijn ook de Chebyshev-veeltermen genoemd, die hij vond als oplossingen van een differentiaalvergelijking.

Dit zijn de eerste zes Chebyshev-veeltermen:

                  

                

Als je nu in de n-de veelterm x vervangt door cos α, dan bekom je een formule voor cos nα:
 
cos 2α = T₂(cos α) = 2cos² α  – 1
cos 3α = T₃(cos α) = 4cos³α  –  3cos α
cos 4α = T₄(cos α) = 8cos⁴ α – 8cos² α + 1
cos 5α = 16cos⁵ α – 20cos³ α + 5cos α
enzovoort ...

Het onderstaande driehoekig schema geeft een middel aan om de coëfficiënten te bepalen.

Elk getal uit de driehoek bekom je door vanaf die positie

alle getallen op de diagonaal naar rechtsboven bij elkaar op te tellen

en hiervan dan alle getallen op de diagonaal naar linksboven af te trekken.

Zo is bijvoorbeeld 18 = 5 + 1 + 0 – (-20) – 8.

08-04-2014 om 00:00 geschreven door Luc Gheysens  

DE KNUPPEL IN HET HOENDERHOK



Dit weekend gooide gewezen KU Leuven-rector André Oosterlinck
de knuppel in het hoenderhoek door erop te wijzen dat
"de gemiddelde leraar behoudsgezind is en een te laag intellectueel niveau heeft".

Dat er iets mis is met de lerarenopleiding en met de status van het lerarenberoep valt zeker niet te ontkennen.
Vaak is het beroep van leraar ook al niet meer een eerste keuze.
Maar dat er heel wat plichtsbewuste leraren zijn
die dagelijks enthousiast voor de klas staan,
 mag men zeker ook niet ontkennen!

Vijf voorstellen:



1. Zie toe op de instroom met een vakkengerichte proef en een taalproef.



2. Zorg voor een permanente opleiding en contact met het bedrijfsleven.



3. Bewaak de planlast en geef de leraar meer ruimte om met zijn vak bezig te zijn.



4. Zorg voor een beter beleid.
Vaak heb ik moeten vaststellen dat mensen
die het nu voor het zeggen hebben over onderwijskundige onderwerpen,
'wat vervreemd zijn' van wat er zich op de werkvloer werkelijk afspeelt.



5. Meer zorg (en financiën) voor de schoolgebouwen in het algemeen
en voor de infrastructuur in het bijzonder.

LINK: http://www.deredactie.be/permalink/1.1931580

07-04-2014 om 11:48 geschreven door Luc Gheysens  

Cahier nr. 40 in de reeks publicaties van T³ Vlaanderen is vanaf heden gratis beschikbaar.

Het cahier bevat 20 uitdagende opgaven voor leerlingen van de derde graad.

Je vindt het cahier hier in bijlage en alle vorige cahiers zijn beschikbaar op www.t3vlaanderen.be

Van dit lesmateriaal mag gratis gebruik gemaakt worden

.Maar misschien zorgden andere belevenissen dit weekend al voor een goed gevoel!

Bijlagen:
cahier_40.pdf (1 MB)   

STELLING VAN DE DUBBELE KOORDE



Claudius Ptolemaeus (ca. 87 - 150, Alexandrië)
gebruikte de wiskunde als hulpmiddel voor berekeningen in de astronomie.
In zijn boek Almagest geeft hij een samenvatting van de toenmalige kennis
over de astronomie en stelt hij koordentabellen op
waarmee hij afstanden berekent tussen punten op een cirkel.
In zijn werk vinden we ook enkele merkwaardige en originele stellingen terug
uit de meetkunde en de goniometrie.
Meer hierover lees je in het mooie artikel van Dick Klingens (zie bijlage).

We vermelden hier echter graag een minder bekende stelling
die ik zelf in het vierde jaar van mijn middelbare studies
als oefening meekreeg en toen niet direct kon bewijzen.

Vind jij een bewijs?

Tip. Zet jouw bril even recht op jouw neus en pas de stelling van Ptolemaeus toe voor een koordenvierhoek.

Bijlagen:
Koordentabel van Ptolemaeus.pdf (150.3 KB)   

Wiskundigen gaan soms - louter voor de kick - op zoek naar merkwaardige getallen.

Ik stelde me de vraag of het mogelijk is dat een getal van de vorm G = a^a + b^b + c^c + d^d
(waarbij a, b, c en d alle gehele waarden van 1 tot en met 9 mogen aannemen)
gelijk is aan het getal H = 1000a + 100b + 10c + d (wat we schrijven als abcd).

Met een eenvoudig programma op mijn grafische rekenmachine (zie bijlage)
vond ik al vlug dat er precies één getal hieraan voldoet :




DENKOEFENING
Kan jij het getal G = 10a + b (wat we schrijven als ab) vinden dat gelijk is aan H = (a + b)² ?

Bijlagen:
Programma voor een TI-84.pdf (125.9 KB)   

KAN JE DE VOLGENDE DRIE OPGAVEN
TELKENS IN VIER MINUTEN OPLOSSEN?

Verdeel de gehele getallen van 1 tot en met 12
in vier groepjes van drie getallen
zodat de som van twee getallen uit elk groepje
gelijk is aan
1) het derde getal
2) het dubbele van het derde getal
3) het drievoud van het derde getal.

Applaus voor wie de oplossing telkens in minder dan vier minuten vindt!
De anderen gluren best eens in de oplossing (zie bijlage).

Bijlagen:
DRIE SOMPROBLEMEN.pdf (125.5 KB)   

EEN ONEIGENLIJKE INTEGRAAL MET EEN EIGEN VERHAAL

Bekijk het eens rustig...

04-04-2014 om 00:00 geschreven door Luc Gheysens  

 

PROBLEEM 7

UITVINDING 7

Rond 1850 waren de meeste strijkijzers gewoon platte stukken metaal
die men op een fornuis plaatste om ze op te  warmen.
Vooraan het strijkijzer was er een punt die echter vaak zorgde voor scheuren.
En als het grondvlak van het ijzer niet helemaal proper was
zorgde dit soms voor vuile strepen op kledingstukken.
Daarom bedacht een zekere Mr. Frank Corbets uit New York een strijkijzer op wieltjes.
Het werd in een metalen bakje op het fornuis geplaats om zo de wieltjes op te warmen.

Bijlagen:
COSMOSPROBLEEM 7_oplossing.pdf (215.8 KB)   

DE KWADRATEN VAN DIOPHANTUS

De Griekse wiskundige Diophantus was een buitenbeentje in zijn tijd
(men weet niet precies wanneer hij leefde; wellicht in de derde eeuw na Chr.).
Waar de meeste wiskundigen van zijn tijd zich bezighielden met meetkunde,
was Diophantus bezeten van getallenleer en algebra.
Die werden toen echter nog vaak op een meetkundige manier behandeld.
Zo was bijvoorbeeld een kwadraatgetal niets anders dan een vierkant.

In zijn werk Aritmetica slaagde Diophantus erin enkele mooie eigenschap uit de rekenkunde te bewijzen.

Hieronder staat een voorbeeld ter illustratie
(dat we hier 'vertalen' in de huidige algebraïsche taal).

Als n een willekeurige positief geheel getal is
en x = n²,  y = (n+1)² en z = 2(x + y +1)
dan zijn de volgende zes getallen kwadraatgetallen:
xy + x + y
yz + y + z
zx + z + x
xy + z
yz + x
zx + y.

Voorbeeld.
Voor n = 2 is x = 4, y = 9 en z = 28.
Hiermee bekom je dan de volgende de zes kwadraatgetallen:
49, 289, 144, 64, 256 en 121.

         

 Kan je de eigenschap in het algemeen bewijzen?

02-04-2014 om 00:00 geschreven door Luc Gheysens  

BELPHEGOR
is een demoon en één van de zeven prinsen uit de hel.
Hij verleidt mensen om ontdekkingen te doen waardoor ze rijk (en vaak slecht) worden.
Naar het schijnt is zijn meest actieve periode de maand april.

Het getal van Belphegor is
1000000000000066600000000000001 = 10³⁰ + 666 x 10¹⁴  + 1.

Dit is een priemgetal en een palindroomgetal,
waarbij in het midden het getal van het Beest 666 staat.
Links en rechts hiervan staan 13 nullen
en dat verwijst dan weer naar het ongeluksgetal 13.

Je bent verwittigd!

01-04-2014 om 00:00 geschreven door Luc Gheysens  

   313

Wat is er nu weer bijzonder aan het getal 313?

313 is zelf een priemgetal en een palindroomgetal
313 – 2 = 311, 313 – 2·3 = 307, 313 – 2·3·5 = 283 en 313 – 2·3·5·7 = 103 zijn priemgetallen
10³¹³ + 313 is een priemgetal

   313 is de kleinst mogelijke magische constante bij een magisch priemvierkant van orde 5.

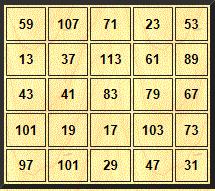
Bron: http://www.magic-squares.net/primesqr.htm#Orders

In de rij van de Fibonaccigetallen (1, 1, 2, 3, 5, 13, 21, 34, 55, 89, 144, 233 ...) is 144 het grootste kwadraatgetal
en in de rij van de Pellgetallen (0, 1, 2, 5, 12, 29, 70, 169, 408 ...) is 169 het grootste kwadraatgetal
en 144 + 169 = 313.

313 is de nummerplaat van de wagen waarmee Donald Duck rondtoerde.

En vandaag is het 31-3!

31-03-2014 om 00:00 geschreven door Luc Gheysens  

PELLGETALLEN

De Pellgetallen zijn genoemd naar de Engelse wiskundige John Pell (17de eeuw)
en worden gedefinieerd door de volgende recursiebetrekking:

Deze rij begint dus met 0 en 1 en elk volgend getal bekomt men
door tweemaal het vorige getal op te tellen bij het getal daarvoor.
 
De rij begint dus als volgt:  0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2 378...

Het n-de Pellgetal is bepaald door de volgende uitdrukking:

Bron: Wikipedia.



In de bijlage kan je zien hoe je de bovenstaande uitdrukking
voor het n-de Pellgetal kunt vinden.

En op de onderstaande figuur hebben we geprobeerd de rij van de Pellgetallen te 'visualiseren'.

Lees ook eens de bijlage waaruit blijkt dat men zowel de Fibonaccigetallen als de Pellegetallen met een grafische rekenmachine kan genereren.

Bijlagen:
Algemene uitdrukking van de Pellgetallen.pdf (214.9 KB)   
FIBONACCI EN PELLGETALLEN.pdf (204.6 KB)   

Om een stelsel van n lineaire vergelijkingen op te lossen
waarbij de determinant van de coëfficiëntenmatrix verschillend is van nul
bestaat er een elegante oplossingsmethode die gebruik maakt van determinanten:

DE REGEL VAN CRAMER

die we hieronder vermelden voor een 3 x 3 - stelsel.

Gabriel Cramer (1704 - 1752) was een Zwitserse wiskundeprof die werkte aan de Universiteit van Genève.
In 1750 publiceerde hij een boek over algebraïsche krommen
waarin hij o.a. bewees dat een vlakke kromme van de n-de graad
in het algemeen bepaald is door n(n+3)/2 punten.
Zo is bijvoorbeeld een kegelsnede (tweedegraadskromme) bepaald door 5 punten. 

In de bijlage bij dit werk publiceert hij een methode om stelsel op te lossen, die nu bekend staat als de regel van Cramer.
Hiermee gaf hij een aanzet tot de ontwikkeling van de theorie van determinanten.

Een kort bewijs van deze regel vind je in de bijlage.

Bijlagen:
De regel van Cramer - bewijs.pdf (177.8 KB)   

 

PROBLEEM 8

UITVINDING 8

Deze snelle driewieler was een uitvinding van een zekere
Mr. Vossner uit Philadelphia.
Hij bedacht een ingenieus systeem om de beweging van de pedalen
over te brengen op de grote wielen van deze fiets.
Eén toer met de pedalen resulteerde in twee volledige toeren van de wielen
zodat men terecht kon spreken van een snelle driewieler.

Bijlagen:
COSMOSPROBLEEM 8_oplossing.pdf (216.1 KB)   

EEN MERKWAARDIGE SOM

Een bewijs zonder woorden zie je hieronder!

Bron: Mathematics Magazine, Vol. 62, No. 5 

***********************************************************************************************

Collega Daniël Tant bezorgde me een bewijs 'met woorden':

27-03-2014 om 00:00 geschreven door Luc Gheysens