NUM'ART is een artistiek project bedacht door Luc Janus.

Vandaag 5-3 zet hij een passend getal op een artistieke manier in de kijker.

*********************************************************************************************************

53

Jodium - Luc Janus

***************************************************************************************************************

Jodium is het scheikundig element met atoomnummer 53.

Het element werd in 1811 ontdekt door de Franse wetenschapper Bernard Courtois.

Hij was de zoon van een salpeterproducent (kaliumnitraat, essentieel bestanddeel van buskruit).

Rond die tijd was Frankrijk verzeild geraakt in meerdere oorlogen en de vraag naar buskruit was groot.

Salpeter werd gewonnen uit zeewier dat werd gedroogd, verbrand en de as werd vervolgens gewassen met water.

Om de salpeter verder te zuiveren werd zoutzuur toegevoegd.

Op een dag schoot Courtois uit met het zuur waarbij een wolk van paarse damp opsteeg.

Het viel Courtois op dat de damp neersloeg op koude oppervlakken en daarbij donkere kristallen vormde.

Hij vermoedde een onbekend element te hebben ontdekt,

maar beschikte niet over voldoende middelen om verder onderzoek te verrichten.

Vermaarde wetenschappers en vrienden van Courtois bevestigden dat het om een nieuw element ging,

dat men de naam jodium gaf, verwijzend naar het Griekse woord ioeides

wat violet- of donkerkleurig betekent.

NUM'ART is een artistiek project bedacht door Luc Janus.

Vandaag 3-3 zet hij via een getalspelletje een passend getal even in de kijker.

*********************************************************************************************************

333

Bifurcation - Luc Janus

*****************************************************************************************

GETALSPELLETJE

Neem er even een rekenmachine bij.

Kies drie opeenvolgende getallen tussen 100 en 300.

Vermenigvuldig ze alle drie met 333.

Splits de bekomen uitkomsten telkens in twee groepjes: het getal gevormd door de eerste twee cijfers en door de laatste drie cijfers.

Tel tenslotte telkens de twee bekomen getallen bij elkaar op.

Voorbeeld.

187 x 333 = 62 271 en 62 + 271 = 333

188 x 333 = 62 604 en 62 + 604 = 666

189 x 333 = 62 937 en 62 + 937 = 999.

Welke uitkomsten bekom jij op deze manier met de drie getallen die je hebt gekozen?

En heb je hiervoor een verklaring?

03-03-2016 om 00:00 geschreven door Luc Gheysens  

Prime Problems - Luc Janus

Vandaag nodigen we je uit om drie raadsels over priemgetallen op te lossen.

PRIEMRAADSEL 1

Vind drie opeenvolgende termen uit een rekenkundige rij waarvan het product een priemgetal is.

PRIEMRAADSEL 2

Hoeveel priemgetallen bevat de volgende rij:

9, 98, 987, 9876, ... , 987654321, 9876543219, 98765432198, ... ?

PRIEMRAADSEL 3

Bestaan er 100 opeenvolgende getallen waarvan er geen enkel getal een  priemgetal is? Zo ja, geef zo een rij getallen.

Oplossingen in bijlage.

Bijlagen:
PRIEMRAADSELS opgelost.pdf (47.3 KB)   

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

24

Tempus fugit A - Luc Janus

Tempus fugit B - Luc Janus

 
*********************************************************************************************************

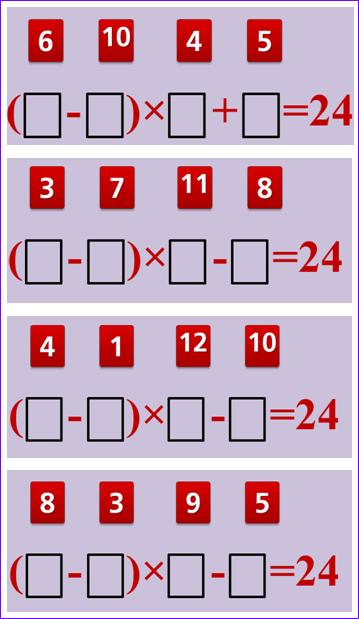
De dagindeling in 24 uur was gebruikelijk bij de Egyptenaren.
24 heeft immers veel delers en dit liet toe de dag in een aantal gelijke delen te verdelen.

De Fransen dachten er ooit aan het tiendelig stelsel ook voor de tijd in te voeren,

maar omdat ze geen internationale steun kregen werden de plannen rond 1900 definitief opgeborgen.

Een Franse klok met een dagindeling van 24 uur en van 10 uur.

*********************************************************************************************************

24 = 4! = 1 x 2  x 3 x 4

24 = 5² – 1² = 7² –  5²

24 = 2⁴ + 2 x 4 = 4² + 4 x 2

Kies een priemgetal p groter dan 3, dan is p² – 1 steeds deelbaar door 24. Weet je waarom?

Het product van vier opeenvolgende natuurlijke getallen is deelbaar door 24. Weet je waarom?

12 oneliners over TIJD

Niets is tijdsverlies als je van de dag geniet  -  auteur onbekend.

Besteed je geld goed, maar besteed je tijd beter  -  E. Hubbard.

Te laat komen is een gebrek aan respect, niet aan tijd  -  Lyda Lombardi.

In het westen hebben ze horloges, maar wij hebben de tijd  -  Afrikaans gezegde.

‘De tijd gaat voorbij’, zeggen we, maar we vergissen ons: de tijd blijft en wij zijn het die voorbijgaan  -  François Raspail.

Aan hardlopen heb je niets. Je moet op tijd vertrekken  -  auteur onbekend.

Tijd die we nemen, is tijd die ons iets teruggeeft  -  Ferstl.

Denk ’s morgens. Handel ’s middags. Eet ’s avonds. Slaap ’s nachts.  -  William Blake.

Alles komt op tijd voor hem die kan wachten  -  Rabelais.

Tijd: dat wat de mens altijd tracht te doden maar wat uiteindelijk hem doodt  -  Herbert Spencer.

De dag van vandaag ziet men pas goed bij het licht van morgen  -  Rémy Montalée.

De tijd heelt alle wonden, maar de littekens blijven  - Eric de Preester.

____________________________________________________________________________________________________

The trouble with life is that there are so many beautiful women and so little time - John Barrymore, Amerikaans auteur

29-02-2016 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

92



In Honour of Dirk Frimout - Luc Janus

Dirk Frimout is een Belgische ruimtevaarder. Hij werd in 1992 de eerste Belg in de ruimte.

Van 24 maart  tot 2 april  cirkelde hij als een van de zeven astronauten met de Spaceshuttle Atlantis 143 keer om de aarde.

22-02-2016 om 00:00 geschreven door Luc Gheysens  

Met dank aan de oogchirurgen van het Ziekenhuis Maria Middelares (Gent, 19-11-2015)

en AZ Groeninge (Kortrijk, 15-02-2016).

   

17-02-2016 om 19:09 geschreven door Luc Gheysens  

Bijlagen:
Sangaku met vier cirkels opgelost.pdf (150.7 KB)   

Arabian Affair - Luc Janus

***********************************************************************************************************

Mohammed ibn Moesa al-Chwarizmi leefde ongeveer van 800 tot 840
en was een van de beroemdste wetenschappers op de gebieden van wiskunde,
geografie en astrologie en van Perzische afkomst.

Het concept van een algoritme in de wiskunde is zijn idee.
Om deze reden wordt hij wel de "grootvader van de informatica genoemd".
Het woord algoritme is trouwens van zijn naam afgeleid.

Verder leverde hij grote bijdragen aan gebieden als algebra,
trigonometrie, astronomie en astrologie, geografie en cartografie.
Zijn systematische en logische aanpak van het oplossen van lineaire en kwadratische vergelijkingen
gaven gestalte aan de algebra, een vakgebied dat zijn naam ontleent
aan Chwarizmi's beroemde boek over het vakgebied:
Hisab al-jabr wa al-muqabala (de theorie van transformatie en herstel).

De term algebra is afgeleid van het Arabische woord al-jabr..

Hij nam het Indische symbool "0" over en introduceerde het gebruik van Arabische cijfers in de wiskunde.
De Arabische cijfers zijn echter ontstaan in India.

Je kunt tenslotte nog even meegenieten van het Abdul Hassan Orchestra

(een idee van de Nederlander Hans van Eijck die eerder al succesvol was met de groep Tee Set)
met de uitvoering van Arabian Affair.

Wanneer begin jij met buikdansen?

15-02-2016 om 00:00 geschreven door Luc Gheysens  

 NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

XXX 


 
Snowmen - Luc Janus

*********************************************************************************************************

********************************************************************************************************

XXX = het getal 30 of het jaar 30 in Romeinse cijfers

xxx = toespeling op harde pornografie, maar ook symbool voor drie kussen

XXX = de drie andreaskruisen in het wapen van Amsterdam sinds de late middeleeuwen



Sommigen menen dat de kruisen staan voor de drie plagen die Amsterdam getroffen hebben,
nl. het water, het vuur en de pest.
Deze symboliek wordt soms echter ook aan de kleuren toegeschreven:
rood is het vuur, wit het water en zwart de pest.
Een andere theorie is dat de drie kruisen staan voor drie doorwaadbare plaatsen in de Amstel.
Voor geen van deze ideeën bestaat enige historische basis.
De drie kruisen vindt men terug op allerlei gebouwen, in vele logo's en ook op de Amsterdammertjes.
Dit zijn paaltjes op een trottoir die dienen om ongewenst parkeren te verhinderen
en om rijbaan en trottoir duidelijk van elkaar te scheiden.



Bron: wikipedia.

*********************************************************************************************************

30 = 1² + 2²  + 3² + 4²  en daarom is 30 een vierkant piramidegetal



30 = 1²  + 2² + 5²

30 = 3 + 3³

30 = 2 x 3 x 5 (product van de kleinste drie priemgetallen)

15-02-2016 om 00:00 geschreven door Luc Gheysens  

Bijlagen:
Het getal van Euler - bewijs.pdf (509.7 KB)   

Sugar Candy - Luc Janus

**************************************************************************************************

Omdat morgen de vasten begint (10-02-2016 = Aswoensdag) trakteren we je nog vlug op een snoepjesraadsel.

SNOEPJESRAADSEL

Riet, Sien en Tine hebben elk enkele snoepjes gekregen.
Riet heeft er r, Sien heeft er s en Tine heeft er t.
Ze weten alleen hoeveel snoepjes ze zelf hebben gekregen,
dat ze er elk een verschillend aantal hebben gekregen en dat 1/r + 1/s + 1/t = 1.

Hoeveel snoepjes hebben ze dan in totaal gekregen?

TIP. Toon aan dat er uit 1/r + 1/s + 1/t = 1 en het feit dat r, s en t drie verschillende (positieve gehele) getallen zijn,

volgt dat er voor het drietal (r, s, t) 10 mogelijkheden zijn, nl.

(3,3,3), (4,4,2), (4,2,4), (2,4,4), (6,2,3),

(6,3,2), (2,6,3), (3,6,2), (2,3,6), (3,2,6).

Uitleg in bijlage.

Bijlagen:
Snoepjesraadsel - 10 mogelijkheden.pdf (203.4 KB)   

 NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

70

Disco - Luc Janus

The seventies zullen op muzikaal vlak voor altijd geassocieerd worden met de disco-rage.

Discoballen, disco lights, kleurrijke outfits en aangepaste discomoves onderstreepten de typische vierkwartsmaat van de discosound.
De commerciële hoogtijdagen van de disco begonnen in de jaren 1973-'74 met de hits
'Never Can Say Goodbye' van Gloria Gaynor (1973) en 'Rock your baby' van George McCrae (1974).
Met de discofilm Saturday Night Fever (met John Travolta en muziek van de Bee Gees) in 1977 was de rage op haar hoogtepunt.

70 is het 7^de  vijfhoeksgetal.

Het n-de vijfhoekgetal bereken je met de formule n(3n – 1)/2

***************************************************************************************************************************************

EEN BIJBELS RAADSEL

    Tien jaar geleden was Jozef drie keer zo oud als Maria.

Over tien jaar zal Jozef nog maar dubbel zo oud zijn als Maria.

Hoe oud is Jozef nu?

***************************************************************************************************************************************

70² = 1² + 2² + 3² + ... + 24² . Ken je de formule voor de som van de eerste n kwadraatgetallen 1²  + 2² + ... + n² ?

70 = 3² + 5² + 6² = 1² + 2² + 4² + 7²

2⁷⁰ = 1 180 591 620 717 411 303 424 en de som van de cijfers van dit getal is precies gelijk aan 70.

ZOEKERTJE. Die eigenschap is ook geldig voor één  ander getal van de vorm 2ⁿ, met n een geheel getal kleiner dan 10.
Weet je voor welk getal n?

***************************************************************************************************************************************

WEETJE.
Een veldhockeywedstrijd, een korfbalwedstrijd op het veld 
en een voetbalwedstrijd die 20 minuten voor tijd wordt afgefloten
duren 70 minuten.

***************************************************************************************************************************************
Een toemaatje voor de liefhebbers van balletmuziek of van de Bee Gees
of van de moves van John Travolta of van The Minions ...

08-02-2016 om 10:38 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

13

Casino Royal - Luc Janus

****************************************************************************************************************

In een normaal kaartspel zitten er 13 kaarten van de vier kleuren: klaveren, ruiten, harten en schoppen.

Oorlog wordt vaak vooral geassocieerd met geweld, veldslagen en veel actie.

In de realiteit bestaat een groot deel van een oorlog nochtans uit wachten in kampen, loopgraven en hospitalen.

Om verveling tegen te gaan werden vaak kaartspelletjes gespeeld.

Speelkaarten werden niet enkel gebruikt om de tijd te verdrijven.
Deze kaarten hadden tijdens de Eerste Wereldoorlog ook een educatieve functie.
In de eerste plaats werden speelkaarten gebruikt om een andere taal aan te leren.
Door het uitbreken van deze oorlog waren verschillende landen genoodzaakt om samen te werken.
Om de communicatie vlot te laten verlopen konden soldaten via speelkaarten
basiswoorden en zinnetjes in het Frans of Engels leren.
Speelkaarten met de vlaggen en kleuren van de verschillende legereenheden die meevochten in deze oorlog,
zorgden ervoor dat soldaten wisten tegen wie en met wie ze samen vochten.
Ook morse en het aangeven van seinen kon aangeleerd worden via speelkaarten.
Ten slotte kon de militaire kennis ook verbeterd worden
doordat speelkaarten werden uitgegeven met daarop de verschillende schepen van de marine.

Bron: wikipedia.

****************************************************************************************************************

Via het onderstaande filmpje kan je een eenvoudige truc met 52 kaarten aanleren.

Je gaat hiervoor als volg te werk.

Leg eerst 26 kaarten met de beeldzijde naar boven op tafel en onthou welke de 7de kaart is.
Schrijf dat eventueel op een blaadje papier dat je niet toont aan de anderen.
Stop de 26 getoonde kaarten weer onder de resterende 26 kaarten.

De kaart die jij in gedachten hebt genomen (en die op het blaadje papier vermeld is)
zit dus nu op positie 33 in de stapel van 52 kaarten.

Volg dan de werkwijze die in het filmpje wordt gevolgd.

Kan je verklaren waarom de laatste kaart die zal gedraaid worden (in het filmpje is dat klaveren 7)

precies de kaart die jij in gedachten hebt genomen en die op het blaadje papier is vermeld?



Hint.  (10 – a + 1) + (10 – b + 1) + (10 – c + 1) + (a + b + c) = 33.

05-02-2016 om 00:00 geschreven door Luc Gheysens  

Voorbeeld. 
We maken de berekening van de ABSI-index 
voor een vrouw van 1,73 m en 70 kg
met een taille van 75 cm.  

T = 75
BMI = 23.4 en BMI tot de macht 2/3-de = 8,18
L = 173 ten L tot de macht 1/2-de = 13,15
ABSI = 75 / (8.18 x 13.15) = 0,70 (afgeronde waarde).

Wat is nu de betekenis van die 0,70 ?

1 of 100% staat voor de gemiddelde kans die iemand heeft om te overlijden aan de gevolgen van overgewicht.
2 of 200% betekent dus dat iemand 2 maal zoveel kans heeft om hieraan te overlijden.
De 0,70 van deze vrouw betekent dus dat ze een kleinere kans dan gemiddeld heeft (70%) om hieraan te overlijden.

Omdat deze formule eerder ingewikkeld is, zal de BMI wellicht niet zo gauw plaats ruimen voor de ABSI.
Maar men mag verwachten dat bijvoorbeeld diëtisten wel zullen verwijzen naar de ABSI.

En je kunt jouw ABSI-cijfer ook eenvoudig op deze website laten berekenen:
http://www.absicalculator.eu/

04-02-2016 om 22:28 geschreven door Luc Gheysens  

 NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

77

Pentagon - Luc Janus

Een leuk artikel over sudoku's zit in bijlage. Bron: kennislink.nl.

De oplossing vind je in het (niet eenvoudig maar ingenieus) bewijs van R.L. Graham  (zie bijlage).

Bijlagen:
A theorem on partitions - R.L. Graham.pdf (296.4 KB)   
Sudokus ontcijferd.pdf (179.3 KB)   

Moet je zeker zelf binnenkort eens proberen!

31-01-2016 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet vandaag een passend jaartal op een artistieke manier in de kijker.

****************************************************************************************

1933

Weimar - 1933

****************************************************************************************

Von Hindenburg en Hitler (1933)

1933 is een priemgetal, maar ook een bijzonder jaar in de geschiedenis.

Op 30 januari 1933 benoemde rijkspresident Paul von Hindenburg Hitler tot rijkskanselier.

Hiermee kwam een einde aan de Weimarrepubliek (1918 - 1933), de opvolger van het Duitse keizerrijk.

De naam verwijst naar de stad Weimar waar de republiek in 1919 haar grondwet kreeg.

Op 10 februari zou Adolf Hitler in Berlijn zijn eerste (gedreven!) speech geven als rijkskanselier.

30-01-2016 om 00:00 geschreven door Luc Gheysens  

Ongetwijfeld heb jij ook al eens prentjes over een bepaald thema verzameld.

Het verzamelen van Panini-stickers met de kopjes van de voetbalhelden bleek onlangs nog een rage te zijn.

Een wiskundeleraar had het volgende lumineus idee
om zijn leerlingen warm te maken voor zijn vak (en voor de studie van functies).
Bij elk goed antwoord kregen de leerlingen een kaartje met een tekening die een bepaalde functie visualiseert.
In totaal waren er 10 verschillende prentjes (zie bovenstaande afbeelding).
We nemen aan dat er van alle kaartjes evenveel exemplaren beschikbaar waren
en dat ze lukraak werden uitgedeeld aan de studenten bij een juist antwoord.

Hoeveel keer  moest een leerling dan (gemiddeld) een juist antwoord geven om de 10 verschillende prentjes te verzamelen?

Antwoord. 30 keer. 

De wiskundige uitleg zit in bijlage.

Bijlagen:
Uitleg prentjes verzamelen.pdf (265 KB)   

28-01-2016 om 00:00 geschreven door Luc Gheysens  

DE COMPLOTFORMULE

De opwarming van de aarde een verzinsel, vaccins zijn gevaarlijk
en de maanlandingen hebben nooit plaatsgevonden.
Toch? Welnee.
Bij dergelijke complotten zijn zoveel mensen betrokken,
dat ze al na een paar jaar hadden moeten uitkomen.

Tot die conclusie komt de Britse radioloog en wetenschapspopularisator David Robert Grimes door te rekenen aan drie complotten die écht bleken, zoals de NSA-afluisteraffaire, in 2013 onthuld door David Snowden. Hoe meer mensen op de hoogte zijn van een geheimzinnig complot, des te groter de kans dat iemand uit de biecht klapt. Een relatie, die Grimes vangt in een heuse ‘complotcurve’, met bijhorende wiskundige formule. 

Bron: De Morgen.

27-01-2016 om 11:50 geschreven door Luc Gheysens