COCKTAILRAADSEL

Op een cocktailparty laat men 50 studenten geblinddoekt proeven van 4 verschillende cocktails.
Er wordt hen vooraf gezegd dat één ervan op basis van rum is, één op basis van gin,
één op basis van vodka en één op basis van whisky.
Na het proeven blijkt dat elke student minstens één keer juist heeft geraden;
 10% van de studenten heeft precies één keer juist geraden
en 20% van de studenten heeft precies twee keer juist geraden.
Weet jij  nu ook hoeveel studenten precies 3 keer juist hebben geraden
en hoeveel ze alle 4 juist hebben geraden?

TIP: de oplossing is niet 30% en 40%.

02-06-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*******************************************************************************
73

The Best Number - Luc Janus

*************************************************************************************

Schrijf een getal op van 4 cijfer en schrijf dit getal er nog eens achter

zodat je een getal bekomt van de vorm abcdabcd.

Dit getal is altijd deelbaar door 73.

Voorbeeld. 13571357 : 73 = 185909

Weet je ook waarom zo'n getal steeds deelbaar is door 73?

TETRAËDERGETALLEN

Een tetraëder is een vierzijdige piramide.
Op de bovenstaande afbeelding zie je hoe men dan komt tot de rij van de tetraëdische getallen of tetraëdergetallen
die een uitbreiding zijn van de diehoeksgetallen 1, 3, 6, 10 ... (zie elders mijn blog).

Merk op dat het n-de tetraëdergetal de som is van de eerste n driehoeksgetallen:

1 = 1
1 + 3 = 4
1 + 3 + 6 = 10
1 + 3 + 6 + 10 = 20
enzovoort ...

De driehoekgetallen en de tetraëdergetallen duiken ook op in de driehoek van Pascal.
Het n-de driehoeksgetal D_n en het n-de tetraëdergetal T_n 
zijn immers gelijk aan een binomiaalcoëfficiënt:

In de bijlage leiden we de formule voor T_n af uit het feit dat
T_n = D₁ + D₂ + ... + D_n .

Bijlagen:
Bewijs van de formule voor het n-de tetraëdergetal.pdf (155.7 KB)   

DRIEHOEKSGETALLEN EN KWADRATEN

Hieronder staan de eerste zes driehoeksgetallen afgebeeld
en de algemene formule voor het n-de driehoeksgetal.

Hiermee bewijzen we een eenvoudige eigenschap:
het achtvoud van een driehoeksgetal vermeerderd met één is gelijk aan het kwadraat van een oneven getal.

Kan je dit algebraïsch bewijzen?
Hint.  8T_n + 1 = (2n + 1)²

Hieronder stellen we een 'Grieks' bewijs voor 'zonder woorden'.

Gezien?

28-05-2015 om 10:22 geschreven door Luc Gheysens  

Kan het dat  ½ = 1 ?

Wie zei daar ook weer dat biologie de enige wetenschap is
waarvoor delen hetzelfde is als vermenigvuldigen?

27-05-2015 om 10:28 geschreven door Luc Gheysens  

Stelling van Ptolemaeus en formule voor sin (α + β)

Hieronder zie je hoe de formule voor sin (α + β) direct volgt uit de stelling van Ptolemaeus.

Gesnapt?

27-05-2015 om 00:00 geschreven door Luc Gheysens  

FORMULE VOOR sin(α + β)

Hieronder staat een 'bewijs zonder woorden' voor de somformule

Is dit een algemeen bewijs (d.w.z. voor willekeurige hoeken α en β) ?

Gezien?

26-05-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal  op een artistieke manier in de kijker.

*********************************************************************************************************
181

Crickets - Luc Janus

*********************************************************************************************************

In 1913 botste Ramanujan, het wiskundig genie uit India op een merkwaardige Diofantische vergelijking:

2ⁿ  – 7 = x².

Een diofantische vergelijking is een vergelijking waarbij men zoekt naar positieve gehele oplossingen.

In 1948 loste de Noorse wiskundige Trygve Nagell deze vergelijking op en toonde aan
dat er geen oplosssing voor x bestaat die groter is dan 181.
Hij toonde meteen aan dat er slechts vijf koppels (n, x) aan de vergelijking voldoen:

(3, x₁), (4, x₂), (5, x₃), (7, x₄) en (15, x₅).

Kan je telkens de bijhorende x-waarde bepalen?

*********************************************************************************************************

181 is een palindroompriemgetal (een priemgetal dat achterstevoren gelezen gelijk blijft).

Met 179 vormt 181 een priemtweeling.

181 = 91² – 90² = 9² + 10²

181 =  29 + 31 + 37 + 41 + 43 (de som van vijf opeenvolgende priemgetallen)

*********************************************************************************************************

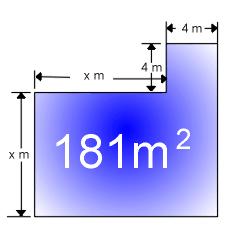
Een klaslokaal (zie onderstaande figuur) heeft een oppervlakte van 181 m².
Kan je de (gehele) waarde van x bepalen zonder rekentoestel?

*********************************************************************************************************

The Crickets (De Krekels) was de begeleidingsgroep van het rock-'n-rollfenomeen Buddy Holly.
De groep had na het wegvallen van Buddy Holly enkele bescheiden hits waaronder dit 'vergeten' My little girl (1963).
The Beatles (beetle = kever) werden bij de naamkeuze van hun groep geïnspireerd door The Crickets, die ze erg bewonderden.
Paul McCartney kocht in 1976 trouwens de rechten op van alle Holly-composities.

25-05-2015 om 10:33 geschreven door Luc Gheysens  

MACHT VAN EEN PUNT T.O.V. EEN CIRKEL - DEEL 2

Ken je nog de definitie en eigenschap van de macht van een punt t.o.v. een cirkel?

In dit tweede deel (gisteren verscheen deel 1) beschouwen we een punt P buiten een cirkel.

Als twee halfrechten vanuit een punt P buiten een cirkel die cirkel respectievelijk snijden en de punten A en B en de punten C en D, dan is .

Dit is uiteraard een direct gevolg van het feit dat de driehoeken PAD en PCB gelijkvormig zijn.

Als C = D is PC een raaklijn aan de cirkel en in dat geval is 

Op het onderstaande plaatje zie je hoe deze laatste formule ook rechtstreeks kunt bewezen worden via de stelling van Pythagoras.

Gezien?

24-05-2015 om 00:00 geschreven door Luc Gheysens  

WISKUNDE EN BEDRIJFSPSYCHOLOGIE
Bron: De Druivelaar

23-05-2015 om 12:07 geschreven door Luc Gheysens  

De onderstaande knippuzzel is een mooie toepassing op de stelling van Pythagoras.

OPGAVE 1.
Met vijf identieke vierkanten maakt men een kruis.
Kan je deze figuur in VIJF stukken knippen
waarmee je dan een vierkant kunt vormen?

OPLOSSING

 

OPGAVE 2.
Kan je het kruis uit opgave 1 ook in VIER stukken knippen
waarmee je weer een vierkant kunt vormen?

OPLOSSING IN BIJLAGE!

Bijlagen:
KNIPPUZZEL.pdf (178.2 KB)   

MACHT VAN EEN PUNT T.O.V. EEN CIRKEL - DEEL 1

Ken je nog de definitie en eigenschap van de macht van een punt t.o.v. een cirkel?

In dit eerste deel (morgen volgt deel 2) beschouwen we een punt P binnen een cirkel.

Als de koorden [AB] en [CD] van een cirkel elkaar snijden in een punt P, dan is .

Dit is uiteraard een direct gevolg van het feit dat de driehoeken APD en CPB gelijkvormig zijn.
Maar wat kan je dan zeggen over de koorden [AD] en [CB]?
Welnu, stel dat de cirkel een ronde vijver zou voorstellen en dat twee roeiers tegelijk vertrekken uit A en C.
Als hun snelheden zo zijn dat ze in P zouden botsen met elkaar, dan zouden ze,
wanneer ze gelijktijdig uit A en C vertrekken en respectievelijk naar D en B toe roeien ook gelijktijdig in D en B arriveren.

Kan je dat bewijzen?

Op het onderstaande plaatje zie je nog hoe via  'een bewijs zonder woorden' de cosinusregel (voor een scherphoekige driehoek)
volgt uit de hierboven vermelde eigenschap van het macht van een punt (hier het punt M) t.o.v. een cirkel.

Gezien?

23-05-2015 om 00:00 geschreven door Luc Gheysens  

PTOLEMAEUS EN DE COSINUSREGEL

De fameuze (en een beetje vergeten) stelling van Ptolemaeus voor een koordenvierhoek luidt als volgt:

In een koordenvierhoek is het product van de lengtes van de diagonalen gelijk aan
de som van de producten van de lengtes van de paren overstaande zijden.

 

Voor het bewijs volstaat het 4 keer de cosinusregel toe te passen:

op Δ ABD en  Δ BCD waarbij ∠ BAD en ∠ DCB supplementaire hoeken zijn

en op Δ ABC en  Δ CDA waarbij ∠ ABC en ∠ CDA supplementaire hoeken zijn.

Door hieruit telkens de cosinussen te elimineren vind je uiteindelijk (reken maar eens na!) dat

Door deze uitdrukkingen tenslotte lid-aan-lid met elkaar te vermenigvuldigen, bekom je de gewenste formule.

****************************************************************************************************

En zie je ook op het onderstaande plaatje hoe via  'een bewijs zonder woorden' 

 de cosinusregel (voor een stomphoekige driehoek) volgt uit de stelling van Ptolemaeus?

   

22-05-2015 om 00:00 geschreven door Luc Gheysens  

GRIEKSE VERSIE VAN HET KRUISPRODUCT

De Griekse wiskunde was van oorsprong 'meetkundig'.

Men had dus voor heel wat algebraïsche eigenschappen een visuele verklaring.

De welbekende eigenschap voor het kruisproduct

krijgt via het onderstaande plaatje 'een Griekse' verklaring:

als de richtingscoëfficiënt van AB gelijk is aan die van BC dan hebben de groene en de blauwe rechthoek dezelfde oppervlakte!

Met dank aan Martin Kindt.

21-05-2015 om 11:33 geschreven door Luc Gheysens  

Onder het motto 'de (wiskunde)boog kan niet altijd gespannen staan' serveren we je vandaag een ludieke quiz.
Wie 4 van de 8 vragen juist kan beantwoorden is meteen geslaagd!
 
Bron: www.alle-tests.nl/quiz28/quiz/1282066087/s-Werelds-makkelijkste-quiz.
Daar vind je ook de juiste antwoorden

En ja, een quiz winnen kan een mens blij maken!

19-05-2015 om 15:48 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************
3

 The third man - Luc Janus

*********************************************************************************************************

3 dimensies (en misschien wel de tijd als vierde dimensie ?)

3 aggregatietoestanden: vast, vloeibaar en gas.
Ken je ook de juiste benamingen voor de overgang van de ene naar de andere toestand?

De astronoom Edwin Hubble bedacht een systeem om de verschillende vormen van sterrenstelsels in te delen.
Het systeem kent drie hoofdgroepen: E: elliptische stelsel, S: spiraalstelsels, SB: balkspiraalstelsels.
Daarnaast zijn er nog sterrenstelsels die niet aan bovenstaande vormen voldoen,
deze worden Ir (van Irregular, onregelmatig): onregelmatige sterrenstelsels of Pec (van Peculiar, eigenaardig) genoemd.

*********************************************************************************************************

Een melkstoeltje heeft maar drie poten en is daarom het meest stabiele stoeltje:
ook als één poot wat korter is dan de andere blijft het toch staan zonder te wiebelen.

Als men in onderwijsmiddens spreekt van 'competenties',
dan heeft men het over kennis, attitudes en vaardigheden
die meteen de drie poten symboliseren voor een evenwichtige aanpak van de leerplannen.

*********************************************************************************************************

The third man is een Engelse film noir uit 1949 van regisseur Carol Reed met onder meer Joseph Cotten, Orson Welles en Alida Valli.
De muziek, die werd geschreven en uitgevoerd door Anton Karas op citer,
maakt de spanning van de thriller extra dreigend en werd welhaast even klassiek als de film zelf.
De achtervolging in de riolen van Wenen is een legendarische filmscène.

Bekijk je nog eens een stukje uit deze film (Harry Lime thema) met één van de beroemdste katten uit de filmwereld?

18-05-2015 om 07:53 geschreven door Luc Gheysens  

DRIE EENVOUDIGE PROBLEMEN

Hoe verdeel je een willekeurige scherphoekige driehoek in drie gelijkbenige driehoeken?

Niet zo moeilijk: verbind het middelpunt van de omgeschreven cirkel met de drie hoekpunten en klaar is Kees!

Hoe verdeel je een willekeurige scherphoekige driehoek in zes gelijkbenige driehoeken?

Hiervoor kan je de ingeschreven cirkel gebruiken en veel uitleg is er wellicht niet meer nodig.

Maar hoe kan je nu een willekeurige scherphoekige driehoek in vier gelijkbenige driehoeken verdelen?

Zie jij dat zitten?

Bijlagen:
Oplossing van het derde probleem (zonder woorden).pdf (52 KB)   

STAP DOOR EEN A4-BLAD

Kan je in een A4-blad een gat knippen dat groot genoeg is om er doorheen te stappen?

Op het eerste gezicht zou je denken dat dit onmogelijk is, maar
paradoxaal genoeg bestaat hiervoor een ‘wiskundige’ oplossing.

Bron: www.natuurkundeproefjes.nl

En heb je zelf al ooit een papieren Möbiusband gemaakt? De onderstaande website zet je op weg.

http://www.kennislink.nl/publicaties/de-vorm-van-een-mobiusband

Welke mieren kruipen in of op de Möbiusband? 

© The M.C. Escher Company B.V, Baarn

14-05-2015 om 12:38 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij tekens een getal op een artistieke manier in de kijker.

*******************************************************************************************************

360

It turns out -  Luc Janus

Vier rechte hoeken geven 360°.
3 x 60° levert dan weer een gelijkzijdige driehoek op.

Bij de Babyloniërs telde een jaar met 12 maanden van 30 dagen.
Ze lagen hiermee aan de basis van het feit dat een volledige cirkel (een volle hoek) overeenkomt met 360°.

**********************************************************************************************************************************

Aroud the world in 360 degrees
http://www.modernmotodiaries.com/#!about-alex/cb36

Drie jaar deed de motorfanaat Alex Chacon erover
om zichzelf via selfies met een perspectief van 360°
over heel de wereld in de kijker te plaatsen.
Ja, er zijn  nog rijke jonge mensen ...

 

11-05-2015 om 09:33 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

**********************************************************************************************
5

Pentagon - Luc Janus

*****************************************************************************************************

5 zintuigen

5 smaken: zout, bitter, zoet zuur en umami

5 is het vijfde Fibonaccigetal

5 vingers aan een hand, 5 tenen aan een voet (nou ja ...)

5 regelmatige veelvlakken

Bij elk pythagorees drietal (drie positieve gehele getallen a, b en c met a² = b² + c²) is minstens één getal deelbaar door 5

************************************************************************************************************

De stelling van de vijf cirkels (Auguste Miquel, 1838)

Info op http://www.vandeveen.nl/Wiskunde/Cirkels/5_cirkel_stelling_van_Miquel.html

************************************************************************************************************

En misschien moet een succesvolle popgroep als Five terug eens opduiken in onze examenlokalen.

11-05-2015 om 00:00 geschreven door Luc Gheysens