NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal (en soms ook twee getallen) op een artistieke manier in de kijker.

*********************************************************************************************************

6 en 9

Foetus - Luc Janus

 

Na 6 maanden gaan de neusgaten bij een foetus open en begint hij voor het eerst wat te ademen.
Ook duimzuigen is vanaf nu een vaak voorkomende activiteit.
Men kan vanaf de zesde maand ook duidelijk de hartslag horen.
Dat de toekomstige moeder tussen de 6^de en 9^de maand van de zwangerschap in beweging blijft,
komt het kind alleen maar ten goede.

De gemiddelde zwangerschap duurt 38 weken of ongeveer 9 maanden (of 'negen manen').
Op http://www.24baby.nl/zwanger/ben-ik-zwanger/uitgerekende-datum-berekenen/
kan je de vermoedelijke datum van de geboorte berekenen.

26-07-2015 om 00:00 geschreven door Luc Gheysens  

 

Via een eenvoudige rekensom leiden we (in 2015) jouw leeftijd af
uit het aantal pralines dat je eet!

STAP 1.  Hoeveel pralines zou jij nu kunnen opeten? Noteer het aantal (een getal van 1 tot en met 9).
STAP 2. Vermenigvuldig dit getal met 2 en noteer de uitkomst.

STAP 3. Tel hier eerst 5 bij op en vermenigvuldig daarna het resultaat met 50. Noteer de uitkomst.

STAP 4. Tel hierbij 1765 op als je dit jaar reeds jarig bent geweest. Tel 1764 op als je verjaardag nog moet komen.
STAP 5. Trek nu van het bekomen getal jouw geboortejaar af.

26-07-2015 om 00:00 geschreven door Luc Gheysens  

Casper en Hobbes © Bill Watterson

Veel mensen geraken gefascineerd door vaak eenvoudige spelletjes
waarbij de 'goochelaar' er schijnbaar probleemloos in slaagt een getal of een symbool te raden dat iemand in gedachten heeft genomen.
Op het internet circuleren een aantal dergelijke goocheltruuks.

We presenteren er hier eentje via een Franstalige powerpointpresentatie.

PS. Een Nederlandstalige versie hiervan zit in bijlage.

Men vraagt je verschillende keren na elkaar een getal van twee cijfers in gedachten te nemen en hiervan de som van de cijfers af te trekken.
Kies je bijvoorbeeld 43, dan bereken je 43 – (4 + 3) = 43 – 7 = 36.
Dan toont de Grote Kissetou een tabel met getallen en Egyptische symbolen en vraagt je het symbool te onthouden dat correspondeert met het getal 36.
En blijkbaar slaagt de Grote Kissetou er keer op keer in het gekozen symbool te raden!

Bijlagen:
De grote Kissetou.ppt (2 MB)   

Vandaag 22/7 dringt een acute vraag zich op:

is π groter of kleiner dan 22/7?

Een verrassend antwoord krijg je via de berekening van een bepaalde integraal.
We maakten de berekening via de 'definite integral calculator' van Wolfram
die je vindt op http://www.wolframalpha.com/widgets/gallery/ (bij de rubriek 'Mathematics').

Aangezien de functie die hier wordt geïntegreerd strikt positief is (f(x) > 0 in [0,1]), is ook 22/7 –  π > 0.

Voor de onbepaalde integraal vond ik de volgende uitdrukking:

22-07-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

Op onze Belgische Nationale Feestdag kan er een speciale bijdragen van af!  

********************************************************************************************************************
21

Fuzzy - Luc Janus

********************************************************************************************************************

21 is een driehoeksgetal (1 + 2 + 3 + 4 + 5 + 6 = 21)

en 21 is het aantal stippen op een gewone dobbelsteen

********************************************************************************************************************

GETALSPELLETJE MET 21

Kies een geheel getal tussen 11 en 99 en vermenigvuldig het met 21.

Laat van de uitkomst het laatste cijfer weg.

Vermenigvuldig het bekomen getal met 11 en trek van de uitkomst het eerder weggelaten cijfer af.

De uitkomst is steeds deelbaar door 21.

Voorbeeld.  59 x 21 = 1239  >>>  123 x 11 = 1353  >>>  1353  –  9 = 1344 >>> 1344 : 21 = 64.

Heb jij een verklaring?

********************************************************************************************************************

Voor wie op 21 juli wat meer wil te weten komen over de complexe politieke structuur van BELGIË
hebben we hier de volgende verklarende bijdrage geplaatst.

Geniet ervan! Profitez-en! Genießen Sie es! Enjoy!

21-07-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal (en soms ook twee getallen) op een artistieke manier in de kijker.

*******************************************************************************************************************

28 en 86

Padovan - Luc Janus

28 en 86 zijn twee niet-opeenvolgende getallen uit de rij van Padovan en ook hun som 114 is een getal uit deze rij.

De rij van Padovan is een rij gehele getallen (P_n) die gedefinieerd wordt

door de beginvoorwaarden: P₀ = P₁ = P₂ = 1 en de recursiebetrekking P_n = P_n-2 + P_n-3 .

De eerste termen uit deze rij zijn 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, ...

De rij is genoemd naar de architect en schrijver Richard Padovan, die zijn ontdekking toeschreef aan de Nederlandse architect Hans van der Laan.

De rij is beschreven door de Britse wiskundige Ian Stewart in zijn column Mathematical Recreations in Scientific American van juni 1996.

Hieronder zie je hoe gelijkzijdige driehoeken, waarvan de zijden de getallen zijn uit de rij van Padovan, een spiraal bepalen.

Bron: Wikipedia.

"De beste manier om chaos te veroorzaken is alles te regelen"

Karel Boullart, filosoof en docent aan de UGent

20-07-2015 om 00:00 geschreven door Luc Gheysens  

17-07-2015 om 14:33 geschreven door Luc Gheysens  

EEN LOGISCH RAADSELTJE

Mevr. Deblauwe, Mevr. Van Geel en Mevr. Lerouge
dragen elk een kleedje in een verschillende kleur:
een blauw, een geel of een rood.
Mevr. Van Geel merkt op dat geen van hen
een kleedje draagt in de kleur waarnaar hun naam verwijst.
"Dat klopt", zegt de dame met het rode kleedje.

Welke kleur heeft het kleedje dan
dat Mevr. Deblauwe draagt?

En ja, je hoeft echt niet over super-talenten te beschikken om dit op te lossen!

 

16-07-2015 om 21:09 geschreven door Luc Gheysens  

15-07-2015 om 18:24 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal  op een artistieke manier in de kijker.

***********************************************************************************************
39

Relativity - Luc Janus

Black Holes - Luc Janus

Einstein toonde het belang aan van de vierde dimensie

en zijn relativiteitstheorie deed de wetenschappers verder dromen over zwarte gaten,

reizen met de lichtsnelheid en de ontdekking van buitenaards leven.

***********************************************************************************************

39 = 3 + 5 + 7 + 11 + 13  (som van vijf opeenvolgende priemgetallen) en 3 x 13 = 39

39 = 20²  – 19²  en 39 = 1³ + 2³ + 3³

1/39 = 0,025641... en 25641 x 39 = 999999,

25641 x 26 = 666666 en 25641 x 13 = 333333.

***********************************************************************************************

"39" is een song van Queen, geschreven en gezongen door Brian May.

Het lied staat op het succesvolle album A Night At The Opera.

''39" vertelt het verhaal van een ruimteschip bemand met vrijwilligers dat de ruimte in gaat op zoek naar een nieuwe bewoonbare planeet.

Wanneer de bemanning terugkeert zijn er 100 jaren verstreken, terwijl zij zelf nauwelijks zijn verouderd.

De ruimtereizigers hebben al hun dierbaren verloren.

Dit gegeven is gebaseerd op een onderdeel van Einstein's relativiteitstheorie (tweelingparadox).

13-07-2015 om 00:00 geschreven door Luc Gheysens  

Nu de Griekse euro meer dan ooit in de kijker staat, mag hier een wiskundige bijdrage erover niet ontbreken.

Onlangs was ik op reis in Griekenland en ontmoette er de Griekse wiskundige Mikis Tuflos.
Hij legde 8 euro's op tafel, vier met de kopzijde naar boven en vier met de muntzijde naar boven.

Mikis werd geblinddoekt en trok een paar handschoenen aan.
Daarna mocht ik de 8 muntstukken door elkaar heen schuiven.

Mikis beweerde dat hij dan geblinddoekt de acht muntstukken in twee groepjes van vier zou verdelen
en dat hij ervoor kon zorgen dat het aantal munten met de kopzijde naar boven
(en dus ook het aantal munten met de beeldzijde naar boven) in beide groepjes gelijk zou zijn.

Tot mijn verbazing slaagde Mikis hier vrijwel onmiddellijk in.
Hoe deed hij dat?



Oplossing in bijlage.

Bijlagen:
Wiskunde met de Griekse euro.pdf (26.3 KB)   

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

Op deze Vlaamse feestdag mag een 'Vlaamse Leeuw' niet ontbreken.  

********************************************************************************************************************
11

The Lion of Flanders - Luc Janus

Robrecht III van Vlaanderen (= Robrecht van Béthune), graaf van Nevers kreeg de bijnaam 'De Leeuw van Vlaanderen'.

Hij ligt begraven in de Sint-Maartenskathedraal in Ieper.

Zelf nam hij geen deel aan de Guldensporenslag, maar bood na 1302 wel verzet aan de koning van Frankrijk.

********************************************************************************************************************

 EEN GETALSPELLETJE MET 11

Neem er even een rekenmachientje bij.

Tik een positief geheel getal in van 6 cijfers, te kiezen uit de cijfers 1, 2, 3, 4 en 5.

Vermenigvuldig het getal met 11.

Schrijf de uitkomst nu achterstevoren op.

Je zult vaststellen dat dit getal zelf weer deelbaar is door 11

en bij deling ervan door 11 bekom je een quotiënt dat precies gelijk is aan het oorspronkelijke getal achterstevoren.

Voorbeeld. 452153 x 11 = 4973683 en 3863794 : 11 = 351254.

Kan je dit verklaren?

********************************************************************************************************************

En dan was er in 2008 nog de opgemerkte 'nieuwjaarsconférence' van de toenmalige Franse premier Nicolas Sarkozy...

11-07-2015 om 00:00 geschreven door Luc Gheysens  

Cirkels hebben niet enkel een perfecte vorm, meer heel wat verrassende eigenschappen.
De volgende merkwaardige stelling over 4 punten op een cirkel is daar de perfecte illustratie van.

Meteen mijn favoriete stelling over cirkels!

Een bewijs hiervan vind je in bijlage.

Bijlagen:
EEN MERKWAARDIGE CIRKELSTELLING.pdf (212.4 KB)   

Ziehier een leuke getallenpriramide
voor liefhebbers van rekensommen met derdemachten!

1 =  1³
   2 + 3 + 4 = 9 = 1 + 8 = 1³ + 2³ 
5 + 6 + 7 + 8 + 9 = 35 = 8 + 27 = 2³ + 3³
10 + 11 + 12 + 13 + 14 + 15 + 16 = 91 = 27 + 64 = 3³ + 4³
17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 = 189 = 64 + 125 = 4³ + 5³

enzovoort ...

Op de n-de rij staat dan de som
(n²  –  2n + 2) + (n² – 2n + 3) + ... + n²
die volgens de formule voor de som van 2n   –  1 opeenvolgende termen uit een rekenkundige rij
gelijk is aan (n² – 2n + 2 + n²)(2n   –  1)/2 = 2n³   –  3n² + 3n   –  1
en dit is precies gelijk aan (n   –  1)³ + n³.

Leuk om te weten:  (4 + 9 + 1 + 3)³ = 4913.

1³ = 1, 2³ = 8, 3³ = 27, 4³ = 64 ...  worden soms ook de kubusgetallen genoemd.
Ze komen op een natuurlijke manier te voorschijn
wanneer je opeenvolgende oneven getallen bij elkaar optelt:

06-07-2015 om 15:22 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal (en soms zelfs twee getallen) op een artistieke manier in de kijker.

***********************************************************************************************
28 en 85

Funny - Luc Janus

GRAPPIG FEIT 1.

Het 'spiegelbeeld' van 85 is 58, maar het kan ook 28 zijn.

85 en 58 zijn beide Smithgetallen. Dit zijn getallen waarvan de som van de cijfers

gelijk is aan de som van de cijfers van de priemfactoren waarin je die getallen kunt ontbinden:

85 = 5 x 17 en 5 + 1 + 7 = 13 en ook 8 + 5 = 13

58 = 2 x 29 en 2 + 2 + 9 = 13 en ook 5 + 8 = 13.

GRAPPIG FEIT 2.

28 = 7 x 13.

Een verklaring komt van het komisch duo Abbott en Costello.

06-07-2015 om 00:00 geschreven door Luc Gheysens  

Menig dwalende wiskundige komt op een zondagse zoektocht
naar opflakkeringen van mathematische hilariteit
wel eens bij de pi-kante exploten van Drs. P terecht.

Deze eigenzinnige en creatieve zanger en tekstdichter overleed op 13 juni 2015.

Zijn ongeëvenaarde taalkunstige zangerigheid zorgt nu
voor een pakkende en beklijvende Griekse tango (meteen een actueel Europees probleem)
tot meerdere eer en glorie van wat wij in een getal met de decimale kwaliteiten van 3,14159... proberen te vatten.

En zijn we allen niet ergens een beetje een neuro-, fana-, roman-, mys- of mathematicus?

05-07-2015 om 00:00 geschreven door Luc Gheysens  

T

Wiskunde Olympiade bekroond
voor promotie wetenschap bij jongeren

De twee wiskundigen achter de Vlaamse Wiskunde Olympiade krijgen een loopbaanprijs
voor wetenschapscommunicatie omwille van hun inspanningen
om wetenschap te promoten bij het grote publiek.

De Koninklijke Vlaamse Academie van België voor Wetenschappen en Kunsten
reikt elk jaar een onderscheiding voor wetenschapscommunicatie uit.
Die gaat dit jaar naar professor Paul Igodt van de KU Leuven
en professor emeritus Frank De Clerck van de UGent.
De twee wiskundigen organiseren samen de Vlaamse Wiskunde Olympiade, de wedstrijd die in 2015 dertig jaar bestaat.

“De olympiade en deze wedstrijden activeren jaarlijks meer dan 80 000 kinderen en jongeren
in een inclusieve setting voor het oplossen van aantrekkelijke en uitdagende opgaven.
Hierbij primeert wiskundeplezier boven competitie”, prijst de jury.
“De volgehouden inspanningen van Paul Igodt en Frank De Clerck, en dit over de universiteitsgrenzen heen,
 hebben een positieve impact op de beeldvorming rond wiskunde.
Dit werkt vaak door in de studiekeuze en carrière van vele jongeren.
Tot slot heeft de oprichting in 1985 van de succesvolle Vlaamse Wiskunde Olympiade bijgedragen
tot de realisatie van andere communicatieprojecten in wiskunde en wetenschappen.”

Bron: De Standaard

Flemish Math Olympiad - Luc Janus

03-07-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

********************************************************************************************

1881

The Brothers Karamazov - Luc Janus

In 1881 overleed de Russische romanschrijver Fjodor Dostojevski.

Hij werd wereldberoemd door zijn boek De Gebroeders Karamazov,

dat het wedervaren vertelt van vader Fjodor en zijn drie zonen Dmitr, Ivan en Aleksei.

*****************************************************************************************************************

Op 2 juli 1881 werd James Garfield, de 20ste president van de Verenigde Staten van Amerika neergeschoten door een geesteszieke man.

Hij zou op 19 september 1881 aan zijn verwondingen overlijden.

Wiskundigen kennen Garfield vooral omwille van zijn origineel bewijs voor de stelling van Pythagoras.

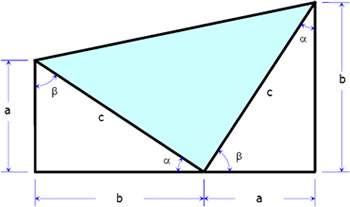
Hij zette hiervoor de onderstaande tekening op papier. De figuur is een trapezium dat is opgedeeld in drie rechthoekige driehoeken.

De oppervlakte ervan kan dan op twee manieren berekend worden en na herleiding vindt men dat c² = a² + b².

*********************************************************************************************************************************

1881 is een Smithgetal omdat het voldoet aan de volgende eigenschap:

de som van de cijfers van het getal is gelijk aan de som van de cijfers van alle factoren die voorkomen in de ontbinding in priemfactoren van dat getal:

1881 = 3 x 3 x 11 x 19  en 1 + 8 + 8 + 1 = 3 + 3 + 1 + 1 + 1 + 9.

Smithgetallen zijn vernoemd door Albert Wilansky van Lehigh University (Pennsylvania) naar zijn schoonbroer Harold Smith.

Wilansky ontdekte in 1982 dat het telefoonnummer 4937775 van Smith deze eigenschap heeft:

4937775 = 3 x 5 x 5 x 65837 en 4 + 9 + 3 + 7 + 7 + 7 +5 = 3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42.

ZOEKERTJE. Bepaal de twee Smithgetallen tussen 20 en 30.

1881 is een apocalytische macht omdat het voldoet aan de volgende eigenschap:

een natuurlijk getal n is een apocalyptische macht als in het getal 2ⁿ (voluit geschreven) drie opeenvolgende cijfers 666 (het getal van het beest) opleveren.

2¹⁸⁸¹ =

02-07-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project van Luc Janus.

 Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

*********************************************************************************************************

XII

Cats of Rhodes - Luc Janus

Tijdens het verblijf op Rhodos hadden we een beetje oog
voor de Griekse mythologie
maar vooral voor de Griekse katten.
Een godengeschenk?

Volgens de Griekse mythologie verenigde Gaea, Moeder Aarde,
zich in het begin der tijden met haar zoon Uranus 
en bracht 12 Titanen voort.

30-06-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

************************************************************
43

Prime world - Luc Janus 

43 is een bijzonder priemgetal.

Het vormt een priemtweeling met 41.

43 = 2 + 5 + 7 + 29

43 = 3 + 17 + 23

43  = 11 + 13 + 19

en in deze drie sommen duiken de eerste 10 priemgetallen op.

************************************************************************************************

43 is het grootste positief geheel getal dat je niet kunt vormen als een som met behulp van de getallen 6, 9 en 20.

Je leert meer hierover via het onderstaande youtube-filmpje. Smakelijk!

29-06-2015 om 21:23 geschreven door Luc Gheysens