Het driehoeksverhaal dat aanvankelijk als trilogie bedoeld was, dreigt te ontaarden in een quintilogie of zelfs een sextilogie. En dat ondanks het feit dat ik het hier over de stelling van Pythagoras niet eens meer hoef te hebben. Als aandachtige lezer van mijn blogs zal het u wellicht niet ontgaan zijn  –  míj was het overigens wél ontgaan – dat ik het daar enkele jaren geleden al eens over gehad heb. Of weet u dat óók niet meer? Of behoorde u toen nog niet tot de zevenkoppige schare van mijn trouwe lezers? Klik dan hier maar op www.bloggen.be/kris/archief.php?ID=170228. 

... [ goed zo, lees nu maar rustig verder ]

En zeg nu eerlijk: vindt u de stelling van Pythagoras niet boeiend? En wat vindt u van de rechthoekige driehoek en van de driehoek in ’t algemeen? Samen met de cirkel toch zeker wel de meest fascinerende figuur uit de vlakke meetkunde. Of niet?

En omdat u nu tóch in de stemming bent... Eén van de mooie opdrachten in de wiskunde is deze: teken een rechthoekige driehoek, alleen gebruikmakend van de basisattributen van de meetkundige, zijnde een passer en een liniaal. Er zijn meerdere methoden, maar deze is mijns inziens de mooiste en de snelste (het vergt hooguit een tiental seconden):

Teken met uw passer een cirkel met middelpunt O. Teken daarin met behulp van de liniaal een middellijn AB. Teken op de cirkelomtrek een willekeurig punt C en verbind dat punt met A en B door middel van een rechte lijn. De driehoek die aldus ontstaat is een rechthoekige. De hele bewerking duurt hooguit tien seconden.

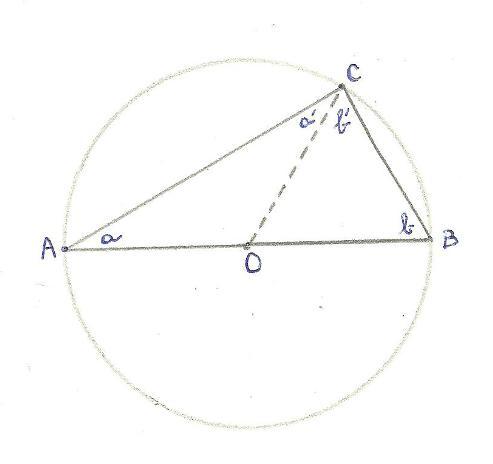
Dat de driehoek wel degelijk een rechthoekige is, valt gemakkelijk te bewijzen via een hulpconstructie, nl. een straal OC, dewelke de rechthoekige driehoek verdeelt in twee gelijkbenige driehoeken (alle “benen” zijn de straal van dezelfde cirkel). Daaruit volgt dat hoek a gelijk is aan hoek a’ en dat hoek b gelijk is aan hoek b’, waaruit volgt dat a + b = a’ + b’. Aangezien de som van de hoeken van een driehoek 180° is, volgt daaruit weer dat de som van a’ en b’ de helft is van 180°, zijnde een rechte hoek.

U hadt dit bewijs, beste lezer, ook best zelf kunnen vinden. Ik heb er u echter de kans niet toe gegeven. En dat wil ik nu goed maken met een zo mogelijk nóg mooiere meetkunde-opgave, in verband met de hierboven getekende rechthoekige driehoek:

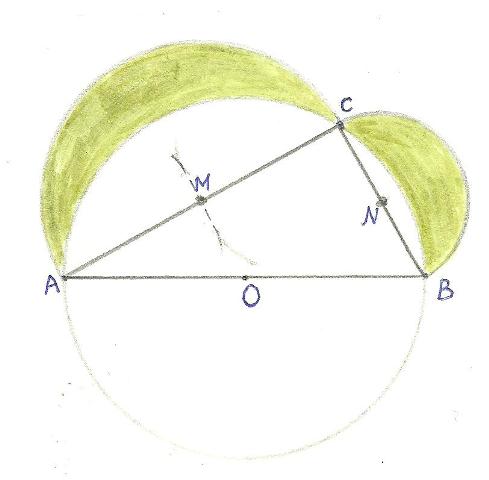
Teken twee cirkels met respectievelijk als middellijn de rechthoekszijde AC en de rechthoekszijde BC (de middelpunten M en N van de beide rechthoekszijden hebt u natuurlijk bepaald volgens de geëigende methode, d.i. met passer en liniaal). De twee cirkels vormen met de cirkel met middellijn AB twee maantjes (ingekleurd). De vraag is nu: is de som van de oppervlakten van die beide maantjes groter of kleiner dan (of misschien wel gelijk aan) de oppervlakte van de driehoek ABC? Mét bewijs.