|
Ik had u, lieve lezer, beloofd dat ik zou doorbomen over de uitkomst van 6 gedeeld door 7, eenrepetitief getal zonder einde. Ach, u zit er wellicht niet op te wachten,
maar voor mij is het een reden om een nieuw woord - quox! - te promoten. Quox (q) is een getal dat dit gemeen heeft met het 6:7-getal dat het evenzeer geen einde heeft, maar evenwel niets repetitiefs
in zich heeft. Zonder een mnemotechnisch middel zie ik geen normaal redelijk schepsel ooit verder komen dan tien, laat staan twintig cijfers.
Ik geef u het getal q even mee (ik beperk mij tot tien cijfers): 1,618033989...
En ik leer u meteen hoe ge er toe komt:
Schrijf op: 1, 2
Tel de 1 op bij de 2, maakt 3
Schrijf op: 1, 2, 3
Maak nu de som van de 2 en de 3, maakt 5
Schrijf nu: 1, 2, 3, 5
Maak nogmaals de som van de laatste 2 getallen, maakt 8
Ge krijgt nu: 1, 2, 3, 5, 8
En nogmaals de som van de laatste twee getallen (13), en zo verder...
Het rijtje wordt: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
Neem nu een willekeurig getal uit dit rijtje en deel het door het getal dat er juist vóór staat. U zal zien dat de uitkomst weinig afwijkt van de quox en dat naarmate
we onze getallen groter kiezen de uitkomst meer en meer de quox benadert...
Het getal pi (3,1415926535...) vertoont wel erg veel overeenkomsten met q: er komt geen end aan en enige repetitiviteit zit er evenmin in. Zelfs de grootste wiskundige genieën ter wereld behelpen zich met een Frans gedichtje als ze meer
dan vijf cijfers na de komma nodig hebben. Het begint als volgt: Que jaime à faire connaître un nombre utile aux sages. Schrijf voor ieder woord het aantal letters op waaruit het bestaat en ziet, daar hebt ge pi, tot tien cijfers na de komma. Met het gedicht kom je echter nog véél verder, ja tot ver boven de duizend
cijfers: het is paginas lang. Voor mij volstaan de tien cijfers na de komma. En als u mij vraagt hoe pi berekend wordt moet ik het antwoord schuldig blijven. Van q weet ik het dus wel, en als u daarnet goed opgelet
hebt weet u het nu dus ook...
Alles goed en wel, zei mijn buurman Firmin, maar zeg mij nu wat de zin is van uw q. Van pi kan je nog zeggen dat het ´t quotiënt is van de cirkelomtrek en de diameter
van die cirkel: exact, tot in het oneindige. Pi kan je tekenen, concreet maken als het ware. Toen heb ik hem verteld dat je precies hetzelfde kunt met quox. Hij stond versteld van mijn uitleg: als
men in een gelijkzijdige vijfhoek een diagonaal (er zijn er zes, identieke) deelt door een zijde bekomt men een quox.
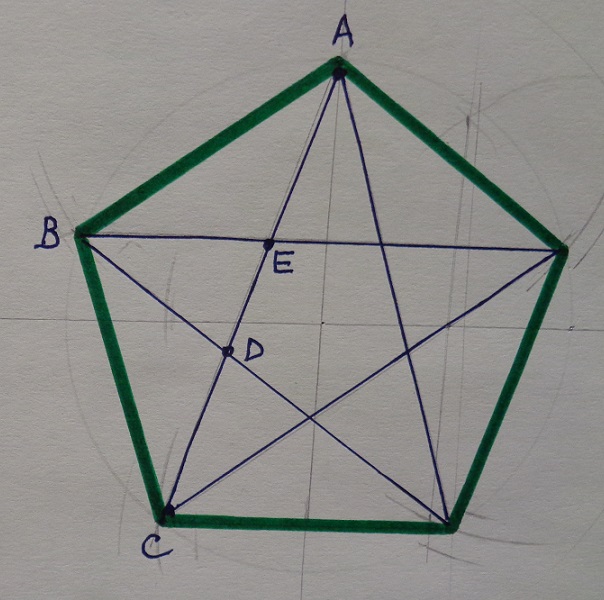
Dus: AC : AB = q
En er is méér: AE : ED = q !
Firmin kon het allemaal nauwelijks geloven.
- Waar hebt gij dat vandaan? vroeg hij.
- Uit een boekje, zei ik.
Hij nam er vrede mee.
Ik liet u al verstaan dat quox een nieuw woord is. Ge zult het tevergeefs zoeken in de Dikke Van Dale. Een paar weken geleden heb ik een partijtje scrabble verloren omdat het woord niet in de Dikke stond. Wacht maar, heb ik toen gezegd, over vijf jaar staat het er wél in! Maar daarvoor, lieve lezers, heb ik uw aller stem nodig. Als u allen, via een mail aan mij gericht, de wens te kennen geeft dat quox opgenomen wordt in ons geliefd woordenboek van de Nederlandse taal, dan lukt het ongetwijfeld wel. Honderdduizend stemmen zijn er nodig.
|



