|
Als u denkt,
beste lezer, dat er een onoverzichtelijke massa reacties binnengekomen is op
mijn verhaal over de verdeling van de cirkel in vijf gelijke delen (m.a.w. de
meetkundige constructie van een regelmatige vijfhoek), dan hebt u het verkeerd
voor. Eén enkele reactie slechts
Maar één die kan tellen! Van niemand minder
dan de geleerde filosoof-mathematicus 0. van Togenbirger. Voluit: professor
Omsk van Togenbirger de Waelekens. Hoelang is het nu geleden dat ik met deze
hooggeleerde man kennis gemaakt heb, te zijnen huize? Hij was toen niet in zijn
gewone doen, zo herinner ik mij. Vanwege een hevige aanval van tandpijn. Of was
het hoofpijn? Migraine of trigeminusneuralgie? Zijn bejaarde moeder leefde nog
en ik weet nog goed dat ik toen een allerhartelijkst gesprek met haar heb
gehad. t Zal een jaar of vijf geleden zijn, als t niet méér is
Sindsdien
hebben onze wegen elkaar niet meer gekruist. Ik wist niet eens of de professor
nog in leven was. Tot gisteren dus. En ik wás al zo verheugd over het feit dat
Lieve Dobbelaere mijn blogs leest. Maar professor O. van Togenbirger!?
Misschien is hij wel één van mijn trouwste lezers. Zal ik nu naast mijn
schoenen gaan lopen? Niet onwaarschijnlijk, lieve lezer, ik ken mijzelf
Of van
Togenbirger de stelling heeft kunnen bewijzen? Bijlange niet. De stelling is
immers niet juist en de verdeling approximatief, veronderstelt de geleerde man.
Ja zeker, hij veronderstelt het, en dat wijst erop dat hij met de jaren
onzekerder is geworden. Vroeger veronderstelde hij nooit iets, hij wist het
gewoon. Maar misschien is hij alleen maar milder geworden. Als de stelling onjuist
is kan vanzelfsprekend niet bewezen worden dat ze wel juist is, nietwaar? Maar
bewijzen dat ze onjuist is, ja, dát zit er misschien wel in, ook volgens van
Togenbirger. Maar tot nader order heeft hij dat niet gedaan. En, hoe gaarne ik
het ook zou doen, kan ik dus, rechtvaardig als ik ben, geen prijs toekennen aan
de professor.
Maar
wat
vloeit mij aan? Pas heb ik deze lijnen geschreven of ik krijg een bericht van
één van mijn trainingsmakkers van Grijsloke met een alternatieve methode om een
cirkel het weze een taart op een geometrisch exacte manier in vijf perfect
gelijke stukken te verdelen. Niet dat ik mij ook nu weer illusies maak, toch
wil ik dit aan u voorleggen:
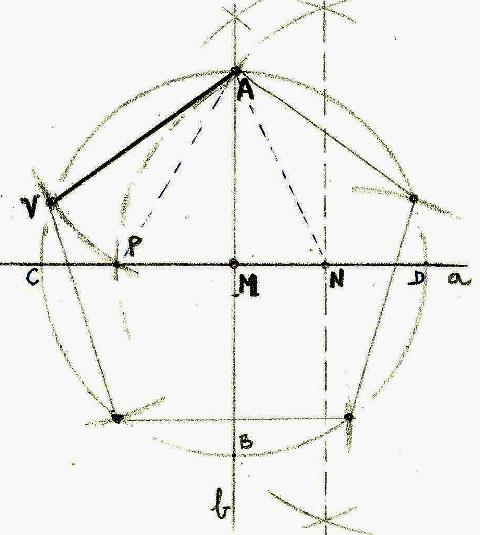
- Teken door het middelpunt M van de cirkel twee loodrecht op elkaar staande middellijnen (a en b); a snijdt de cirkelomtrek in de punten C en D; b doet dat in de punten A en B.
- Bepaal het midden N van het lijnstuk MD.
- Teken een cirkel met middelpunt N en straal AN en bepaal het snijpunt van die cirkelomtrek met het lijnstuk CD; noem dat snijpunt P.
- Teken een cirkel met middelpunt A en straal AP; die cirkelomtrek snijdt onze oorspronkelijke cirkel in een punt V.
- Teken het lijnstuk VA, de eerste zijde van onze regelmatige vijfhoek. De rest volgt vanzelf
Maar ook deze stelling zal wel onjuist zijn. Approximatief. Ik maak mij geen illusies. Een taart verdelen in vijf stukken zal net zo moeilijk blijken als een taart in zeven verdelen. Maar de dag dat we nog met zes zullen zijn wordt het eventjes makkelijk en eenmaal de kaap van de vijf omzeild, zullen alle moeilijkheden voorgoed van de baan zijn. En als er aan t eind nog maar één over zal zijn en er niks meer zal te verdelen vallen
jongens, wat zal ík dan schransen!
|
