|
Eerst wil ik
het hebben over de deelbaarheid van een getal door zeven.
Schrijf de
volgende rij (*) cijfers op:
132645 132645
132645 132
> enzovoort, het patroon is duidelijk.
Neem een
getal waarvan u de deelbaarheid door 7 wilt onderzoeken bv. 146.230.371.
Vermenigvuldig
het laatste cijfer van het te onderzoeken getal met het eerste cijfer van de
rij (*), dus 1 x 1 = 1
Vermenigvuldig
het voorlaatste cijfer van het te onderzoeken getal met het tweede cijfer uit
de rij (*), dus 7 x 3 = 21
Vermenigvuldig
het derde laatste cijfer van het te onderzoeken getal met het derde cijfer uit
de rij (*), dus 3 x 2 = 6
En zo verder
Tel de
uitkomsten op. U bekomt aldus: 1 + 21 + 6 + 0 + 12 + 10 + 6 + 12 + 2 = 70. Als
deze uitkomst deelbaar is door zeven dan is het te onderzoeken getal eveneens
deelbaar door zeven, anders niet. Hier is de uitkomst (70) wel degelijk deelbaar
door 7; 146.230.371 is het dus ook.
Akkoord, het
is vrij ingewikkeld, maar een taart meetkundig exact delen door zeven is niet
alleen veel ingewikkelder, het is zelfs onmogelijk!
Laten we
beginnen met een paar theoretische beschouwingen (we gaan uit van een ronde
taart).
1° Het zoeken van het middelpunt van de taart.
Hiertoe
brengen we twee willekeurige punten aan op de omtrek van de taart (A en B). We
tekenen een loodlijn door het midden van AB, volgens de geijkte methode met
passer en liniaal (cf. fig. 1). We brengen nu nog twee punten aan (C en D) en
tekenen op dezelfde wijze een loodlijn door het midden van CD. De beide
loodlijnen kruisen elkaar exact in het middelpunt (M) van de taart.
2° Het verdelen van een stuk taart in twee gelijke
delen.
Hiertoe
tekenen we de bissectrice van de hoek die de taartpunt vormt (cf. fig. 2). Dat gaat
als volgt
Op de beide benen van de hoek brengen we een punt aan (P en Q), zo
dat beide punten op gelijke afstand liggen van het hoekpunt. We trekken twee
cirkels, met resp. P en Q als middelpunt. De lijn die het snijpunt (S) van de
beide cirkels verbindt met de taartpunt deelt de taart perfect in twee. Die
lijn noemen we de bissectrice.
En nu aan de
slag met het verdelen van onze taart, volgens het aantal personen, zodanig dat
iedereen een even groot stuk krijgt. We bestuderen de verschillende gevallen
afzonderlijk
1° Twee personen (het
minimum, want in het geval van één persoon valt er niets te verdelen, hetgeen
zonneklaar is):
Zie fig. 3.
Iedere rechte lijn door het middelpunt M deelt de taart perfect in twee. De snijpunten van deze lijn met de omtrek van
de taart noemen wij R en L. Het lijnstuk RL noemen we de middellijn. De helft
daarvan is de straal (r), zijnde de afstand van het middelpunt tot elk
willekeurig punt op de omtrek. Poepsimpel, nietwaar?
2° Vier personen:
Zie fig. 4. Via
twee cirkels met dezelfde diameter (groter dan de diameter r van de taart) en
als middelpunt resp. R en L, trekken we een rechte lijn die door het kruispunt
van de twee cirkels loopt en door het middelpunt M van de taart; deze lijn
verdeelt samen met de middellijn RL de taart in 4 gelijke stukken.
3° Zes personen:
Vanuit een
willekeurig punt (W) op de omtrek van de taart tekenen we een cirkel met als
straal r. De snijpunten van die cirkel met de taartomtrek noemen we F en G. De
drie rechte lijnen die resp. door F en M, W en M, en G en M lopen verdelen de
taart in exact zes gelijke stukken. Voor wie een beetje meetkundig inzicht
heeft is dit overigens de logica zelve, m.a.w. zo klaar als niet vertroebeld
pompwater. Zie fig. 5.
4° Acht personen:
Verdelen in
vier (zie fig. 4) en daarna met de bissectrice ieder stuk verdelen in twee
gelijke delen (zie fig. 2).
5° Twaalf personen:
Verdelen in
zes (zie fig. 5) en daarna met de bissectrice ieder stuk verdelen in twee
gelijke delen (zie fig. 2).
6° Drie personen:
Cf. de
verdeling voor zes personen, maar enkel insnijden ter hoogte van de volle
lijnen (zie fig. 6). Iedereen twee zesden geven is een andere mogelijkheid al
blijft er in dat geval méér taart aan het mes kleven.
7° Vijf, zeven, negen, tien en elf personen:
Dat zal nooit
lukken, beste lezer, hoe hard u ook zwoegt, u mag nóg zon meetkundig genie
wezen.
8° En voor méér dan twaalf personen:
Het zal enkel
nog lukken met 16, 24, 32, 48, 64, 96
personen oftewel (ten behoeve van de
bollebozen onder mijn lezers) voor een aantal gasten dat gelijk is aan 2 tot de
n-de macht of 3 maal 2 tot de n-de macht. Maar das onzin natuurlijk. Als er
meer dan twaalf gasten zijn hebt u ongetwijfeld voor méér dan één taart gezorgd.
Of u zou wel een erg krenterig mens
moeten zijn.
Rick en
Willianne zijn alvast geen krenterige lieden. Ze hadden vijf mensen uitgenodigd.
We waren met zijn zevenen. En er waren twéé overheerlijke taarten, afgezien van
al de overige spijzen en dranken die we voorgeschoteld kregen. Het was een
schitterende namiddag op het zonovergoten terras. Een dag zoals april er maar
weinig te bieden heeft. Grollen en grappen onder zeventigers, krank van leden
maar jong en fris van geest. t Had niet beter kunnen zijn. Of toch? Jack
ontbrak. Buiten zijn wil om. Geldig alibi. Met hem erbij had de verdeling van
de taart Erick lang niet zoveel hoofdbrekens bezorgd. Uren lang had hij het
probleem bestudeerd en t resultaat was niet eens helemaal bevredigend (cf.
fig. 7). Met Jack erbij was de verdeling van de taarten een fluitje van een
cent geweest. Hoelang is t geleden dat Jack Vanlichtervelde ons voorgoed
verlaten heeft? Al meer dan vier jaar! De tijd raast voorbij als een hogesnelheidstrein.
Zeventigers sneven bij bosjes. Wie van ons zal er over vier jaar nog over zijn?
Wellicht zal één taart dan ruim volstaan
zal de verdeling van een leien dakje
lopen
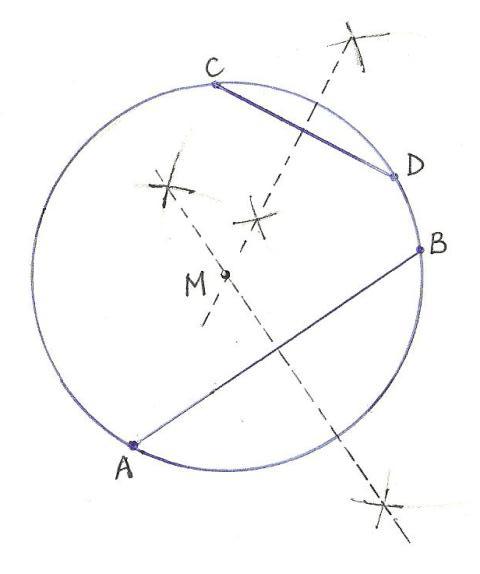 fig. 1 fig. 1
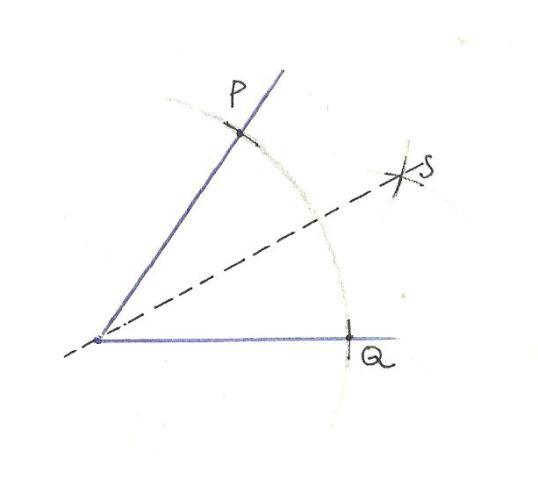 fig. 2 fig. 2
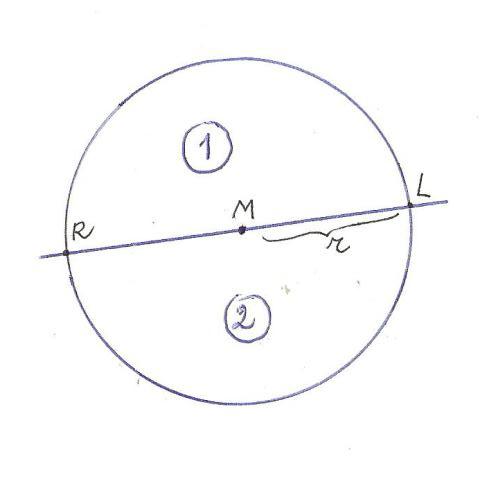 fig. 3 fig. 3
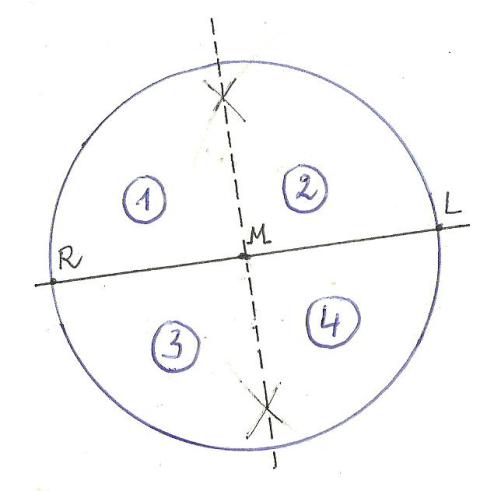 fig. 4 fig. 4
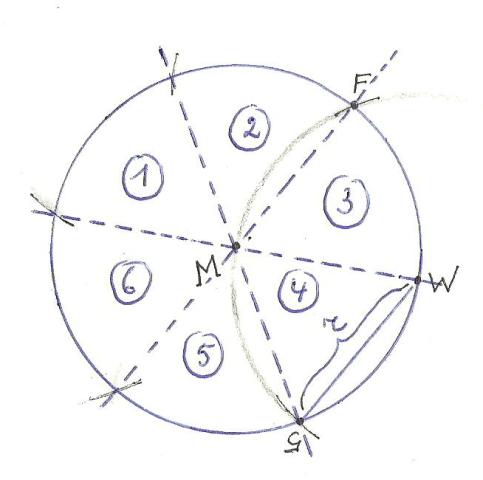 fig. 5 fig. 5
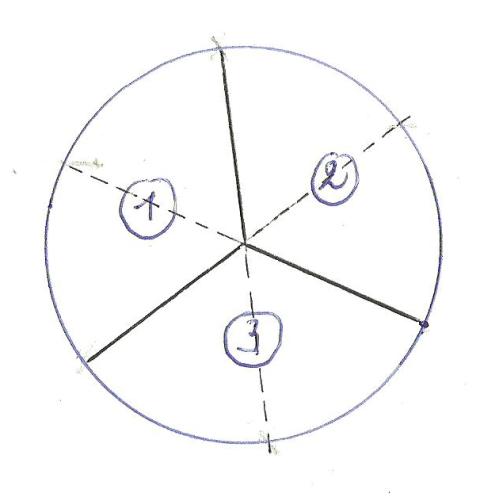 fig. 6 fig. 6
 fig. 7 fig. 7
|



