Bijlagen:
DE GEKNELDE CIRKEL - opgelost.pdf (191.6 KB)   

Bijlagen:
ZESPUNTENCIRKEL.pdf (173 KB)   

Bijlagen:
IN DE JUISTE PLOOI.pdf (174 KB)   

Bijlagen:
Pizza familiale - opgelost.pdf (174.6 KB)   

PARALLELLOGRAM – RECHTHOEK – VIERKANT

Hoe construeer je een vierkant met dezelfde oppervlakte als een gegeven parallellogram?

STAP 1. Construeer een rechthoek met dezelfde oppervlakte als het parallellogram.

STAP 2. Construeer een vierkant met dezelfde oppervlakte als de geconstrueerde rechthoek.
Dit kan via een halve cirkel waarbij b + h de lengte is van de middellijn.
Het lijnstuk met lengte z (op de onderstaande figuur) dat loodrechte staat op de middellijn
is de zijde van het gezochte vierkant.

Hieronder staat nog een 'aanverwante denkoefening' in de vorm van een SANGAKU.

ABCD is een parallellogram. F is een punt op het verlengde van de basis [BC].
E is het snijpunt van AF en de diagonaal BD en G is het snijpunt van AF met de zijde [CD].

Te bewijzen: |AE|² = |EF| . |EG|.

Vind jij hiervoor een bewijs?

Tip. Welke driehoek is gelijkvormig met Δ DEA en welke driehoek is gelijkvormig met Δ AEB?

 Los de opgave daarna met de glimlach op!

21-04-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal (en soms ook twee getallen) op een artistieke manier in de kijker.

*********************************************************************************************************

3 en 4

Yes, you can! - Luc Janus

************************************************************************************************

HET KRUIKPROBLEEM (een gekend dissectievraagstukje)

Op de onderstaande figuur staat een rode kruik afgebeeld.

Kan je die kruik in vier stukken opdelen

waarmee je een vierkant kunt vormen?

En lukt het ook om de kruik in drie stukken te verdelen

waarmee je dan weer een vierkant vormt?

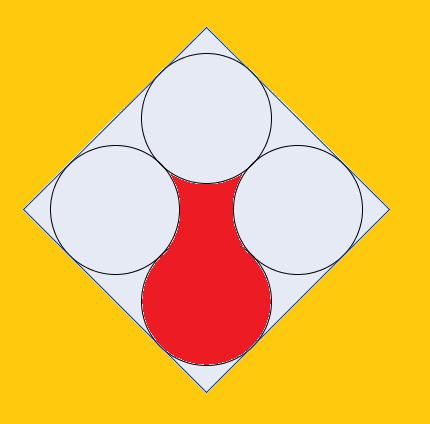
Oplossing(en) in bijlage.

Bekijk ook eens de oplossing die collega Noud Meelen me bezorgde vanuit Tilburg (de kruikenstad!)

************************************************************************************************

Wist je dat ...

elke even macht van een geheel getal ofwel een drievoud is, ofwel 1 meer dan een drievoud?

Voorbeelden.

(-15)² = 225 = 3 x 75
16⁴ = 65 536 = 3 x 21 845 + 1

Wist je dat ...

de vierde macht van een positief geheel getal n vermeerderd met vier, nooit een priemgetal is.

Het is bovendien steeds mogelijk het bekomen getal N = n⁴ + 4 te ontbinden

in twee factoren p en q (p > q), waarbij p – q = 4n (waarbij n het oorspronkelijke getal is).

Voorbeelden.

7⁴ + 4 = 2 405 = 65 x 37 en 65  – 37 = 4 x 7

10⁴ + 4 = 10 004 = 122 x 82 en 122  – 82 = 4 x 10

************************************************************************************************

Bijlagen:
HET PROBLEEM MET DE KRUIK.pdf (92.9 KB)   
Oplossing voor het kruikenprobleem - Noud Meelen.pdf (72.3 KB)   

Le Théorème du Petit Prince

De opgave van vandaag komt van een Kleine Prins vanop zijn asteroïde B 612.

Oplossing in bijlage.

******************************************************************************************************

Is de naam B 612 van de asteroïde vanwaar de Kleine Prins afkomstig is een geheime code?

Misschien verstopte Antoine de Saint-Exupéry hierin de volgende boodschap:
de 6de, 1ste en 2de letter van het alfabet vormen het drieletterwoord FAB (afkorting van 'fabulous') en B leest men als 'be'.
De boodschap luidt dan: BE FABULOUS of probeer op jouw manier 'fantastisch' te zijn.

En de FAB FOUR verklappen je ook nog graag eens hun geheimpje.

Bijlagen:
Le Théorème du Petit Prince.pdf (272.3 KB)