Aristoteles (384 - 322 v. Chr.)
wordt algemeen als de grondlegger
van de logica beschouwd.

Hij stelde zich de vraag wanneer een uitspraak waar is
en kwam tot de conclusie dat dit het geval is
wanneer ze kan afgeleid worden
uit ware uitspraken.

Zo een afleiding noemde hij een syllogisme.

Hieronder staat het meest gekende voorbeeld.

Alle mensen zijn sterfelijk.
Socrates is een mens.
Socrates is sterfelijk.

De eerste twee zinnen in deze redenering noemt men de premissen
en de derde zin is de conclusie.



George Boole (1815 - 1864)
was een Britse wiskundige
die in de 19de eeuw de naar hem genoemde
Booleaanse logica ontwikkelde.

Deze symbolisch logica maakte gebruik van nullen (onwaar) en enen(waar)
en van operatoren (AND, OR, NOT).
Boole legde hiermee meteen de basis
voor de hedendaagse computerwerenschap.

We nodigen je uit om de tekst in bijlage grondig te bestuderen
en de opgaven op te lossen.
Zo leer je meteen hoe de propositielogia,
die erg fundamenteel is voor wiskundige redeneringen en bewijzen,
in elkaar zit.

De opgaven in de bijlage zijn bedoeld als een zelfstudiepakket.
Deze opgaven hoef je dus niet in te dienen!



Aristoteles op de zuidpool:
"Pinguïns zijn zwart en wit.
Oude postkaarten waren zwart en wit.
Pinguïns zijn oude postkaarten."

Bijlagen:
XYT PROPOSITIELOGICA.pdf (308 KB)   

Een logigram of logikwis is een logische puzzel
die je behulp van enkele aanwijzingen moet proberen op te lossen.
Meestal moet je hierbij een aantal zaken of eigenschappen
combineren met de juiste personen.

Je moet hierbij in feite een beetje als een detective te werk gaan 
om via de aanwijzingen de juiste combinaties te vinden.

Om je te helpen om de aanwijzingen op de juiste manier te combineren,
kan je handig gebruik maken van een rooster.
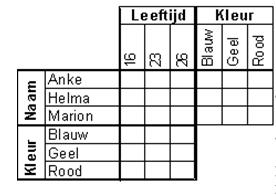
Hieronder staat een dergelijke tabel afgebeeld.

Hierin vul je een plusteken (+) in in een vakje waarvan je weet dat dit een ware combinatie oplevert 
en indien de combinatie onwaar is, vul je een minteken (-) in.

Hieronder geven we een voorbeeld van een logigram,
waarbij het de bedoeling is van drie meisjes hun leeftijd en hun lievelingskleur te ontdekken
aan de hand van de volgend aanwijzingen:

1. Marion is ouder dan Helma.
2. De 23-jarige heeft rood als lievelingskleur.
3. Anke is niet de jongste van de drie en blauw is haar lievelingskleur.



Uit de eerste aanwijzing blijkt dat Marion geen 16 is en Helma geen 26.
Daarom zet een minteken bij (Marion, 16) en bij (Helma, 26).
Wegens de tweede aanwijzing zet je een plusteken bij (rood, 23)
en bijgevolg een minteken bij (blauw, 23), (geel, 23), (rood, 16) en (rood,26).
Door de derde aanwijziging weet je dat er een minteken staat bij (Anke, 16).
Zo weet je meteen dat Helma 16 is.
Er komt wegens de derde tip een plusteken bij (Anke, blauw).
Daarom komt er ook een minteken bij (Anke, geel) en (Anke, rood), (Helma, blauw) en (Marion, blauw).

Door logisch te redeneren los je nu de puzzel verder op.
Bij (Helma, 16) komt een plusteken en bijgevolg een minteken bij (Helma, 23).
Aangezien de 23-jarige rood als lievelingskleur heeft, kan dit niet Helma zijn.
De lievelingskleur van Helma is dus geel.
Dan moet er een plusteken komen bij (Marion, rood) en een minteken bij (Marion, geel).
We weten nu dat Helma 16 is en van geel houdt.
Er komt dus een plusteken bij (geel, 16) en een minteken bij (blauw, 16).
Dan moet een plusteken staan bij (blauw, 26).
Anke is dus 26 en houdt van blauw.
Marion is dus 23 en houdt van geel.
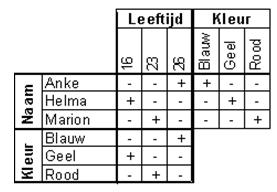
Hiermee is de puzzel helemaal opgelost.

 

Bron: http://members.multimania.nl/puzzel/puzzvb.html

Via opgave 10 in de bijlage dagen we je uit
om zelf een logigram op te lossen!

Bijlagen:
LOGIGRAM.pdf (144.2 KB)   

Is het niet logisch dat een voetbalspeler bij een strafschop rechtstreeks op doel trapt?

Johan Cruijff toonde aan dat dit niet zo logisch is als men op het eerste gezicht zou denken.
Kijk maar!

Met behulp van logica kan men nu ook (voetbal)probleempjes oplossen. Je leert dit in de bijlage.
Meteen schotelen we je via opgave 11 een analoge logische denkoefening voor
die verwijst naar de Vlaamse Junior Wiskunde Olympiade.
Kan je die oplossen?

Bijlagen:
XYT voetballogica.pdf (349.1 KB)   

In de Vlaamse Wiskunde Olympiade
duiken geregeld logicavragen op.

We dagen je uit
om enkele van die opgaven (in de bijlage)
op te lossen.

Voor wie geregeld eens wil oefenen met de vragen
uit de VWO-competitie
biedt het digitaal oefenplatform USolv-IT
heel wat mogelijkheden.
Kies daar de Quick Start
en je kunt meteen aan de slag gaan!
http://www.usolvit.be/usolvit/

Bijlagen:
Logica in JWO.pdf (270 KB)   

Hier vind je het antwoordformulier (aanklikken):
https://docs.google.com/spreadsheet/viewform?formkey=dFpvZUpBS2xpZWdiX1R4eEY4NHduaGc6MQ .

Alle vragen moeten beantwoord worden.
Klik daarna op 'Insturen' (onderaan het formulier).
Meteen worden jouw antwoorden geregistreerd.

Jouw antwoordformulier moet je uiterlijk op 30 april 2012 insturen.
Dank voor jouw deelname!

14-12-2011 om 00:00 geschreven door XYT