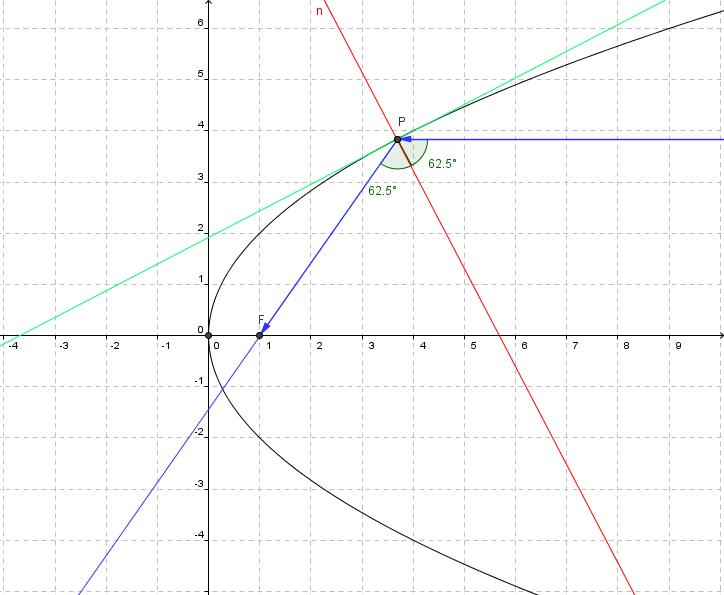
Regelmatig brengen de organisatoren van de VWO (Vlaamse Wiskunde Olympiade) posters op de markt waarop één of ander wiskundig probleem wordt voorgesteld. Voor de editie 2000-2001 verscheen een opmerkelijke poster met een zonnebloem op. Hierbij werd de vraag gesteld waarom zonnebloempitten in het hart van de bloem 21 bochten vormen in de ene richting en 34 in de andere.
Over getallen in de natuur (met dank aan Stéphane Durand, Montreal)
Getallen in de natuur
Waarom hebben bloemen meestal 3, 5, 8, 13, 21, 34 of 55 bloemblaadjes? Enkele voorbeelden: de lelie heeft 3 bloemblaadjes, het boterbloempje 5, de cichorei heeft er 21, het madeliefje vaak 34 of 55, enz.... Als we daarenboven een zonnebloem bekijken, stellen we vast dat de zonnebloempitten twee reeksen bochten vertonen; de éne bochten in de ene richting, de andere in de andere richting. Hierbij is het aantal bochten in de twee richtingen verschillend. Meestal bedraagt het aantal bochten ofwel 21 en 34, ofwel 34 en 55, ofwel 55 en 89, ofwel 89 en 144. Hoe komt dit? Hetzelfde geldt voor denne-appels: waarom vertonen die ofwel 8 spiralen in de ene richting en 13 in de andere ofwel 5 spiralen in de ene richting en 8 in de andere? En tenslotte, waarom heeft een ananas ook 8 diagonalen in de ene richting en 13 in de andere?
Zijn deze getallen puur toeval? Nee! Al deze getallen komen voor in de rij van Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
In deze rij is vanaf het derde getal elke term de som van de vorige twee getallen. Het belang van deze getallen in de natuur was reeds lang opgemerkt, maar pas recent kon aangetoond worden waarom precies deze getallen verschijnen. Dit heeft te maken met efficiëntie gedurende het groeiproces van planten (zie verder).
De verklaring is verbonden met een ander beroemd getal, de gulden snede, dat zelf in verband staat met de spiraalvorm van bepaalde soorten schelpen. Het is wel zo dat bij de zonnebloem, de ananas en de denne-appel de overeenkomst met de Fibonaccigetallen heel exact is, terwijl het bij de bloemblaadjes eerder om een gemiddelde gaat .
De doeltreffendheid van de gulden snede
De hiernavolgende uitleg is heel beknopt. Voor een meer gedetailleerde uitleg verwijzen we naar de website in de referentie.
In veel gevallen is het hart van een bloem opgebouwd uit kleine zaadjes die geproduceerd worden in het midden en die dan naar de rand migreren om uiteindelijk de volledige ruimte op te vullen (zoals bij een zonnebloem, maar op veel kleinere schaal). Elk nieuw zaadje verschijnt onder een bepaalde hoek in vergelijking met het vorige zaadje. Figuur 1 toont bijvoorbeeld het resultaat na verschillende generaties bij een hoek van 90 graden (een kwartdraai).
Uiteraard is dit niet de meest efficiënte manier om de ruimte te vullen. Als de hoek tussen de opeenvolgende zaadjes een deel van een volledige draai is dat overeenstemt met een breuk, 1/3, 1/4, 3/4, 2/5, 3/7, enz..., dan verkijg je altijd een reeks rechte lijnen. Als je dit rechtlijnig patroon wil vermijden, moet je een gedeelte van een volledige draai kiezen dat bepaald is door een irrationaal getal is. Als dit irrationaal getal goed benaderd wordt door een breuk, krijg je een reeks gebogen lijnen (spiraalvormen) die de ruimte niet perfect opvullen.
Om de ruimte optimaal te vullen is het nodig om het "meest irrationaal" getal te kiezen, d.w.z. het getal dat het minst goed wordt benaderd door een breuk. Zo een getal is de gulden snede. De overeenstemmende hoek, de gulden hoek, bedraagt 137,5 graden. (Deze hoek verkrijg je door het niet-geheel deel van de gulden snede te vermenigvuldigen met 360 graden en, omdat je een hoek van meer dan 180 graden verkrijgt, daarvan het complement te nemen). Door gebruik te maken van deze hoek wordt de ruimte optimaal gevuld, d.w.z. dat de afstand tussen alle zaadjes dezelfde is (figuur 3).
Deze hoek moet heel precies gekozen worden: een afwijking van 1/10 graad vernietigt volledig de optimale opvulling van de ruimte. (In figuur 2 bedraagt de hoek 137,6 graden!). Enkel en alleen als de hoek exact de gulden hoek is, zijn er twee reeksen spiralen zichtbaar (één in elke richting): hun aantal stemt overeen met de teller en de noemer van één van de breuken die de gulden snede benaderen: 2/3, 3/5, 5/8, 8/13, 13/21 enz...
Deze getallen zijn precies de getallen uit de rij van Fibonacci (hoe groter de getallen, hoe beter de benadering) en de keuze van de breuk hangt af van de tijdsspanne tussen het verschijnen van de zaadjes in het midden van de bloem.
Dit is de verklaring waarom het aantal bochten in het hart van een zonnebloem, en meer in het algemeen in het hart van bloemen, overeenstemt met een Fibonaccigetal. Bovendien worden de bloemblaadjes gevormd op het uiteinde van één van de reeksen spiralen, waardoor ook het aantal bloemblaadjes, gemiddeld gezien, overeenstemt met een Fibonacci-getal.
--------------------------------------------------------------------------------------------------------------------------------------------------
In hetzelfde jaar verscheen trouwens nog een tweede poster die een verband aangeeft tussen de gulden snede en een huisjesslak.
Bron
www.vwo.be
Bibliografie
De eerste tekst is van de hand van ere-pedagogisch begeleider Walter De Volder en werd door collega's Paul Decuypere en Dominiek Ramboer voorgesteld op de Dag van de Wiskunde van 20 november 2004 in Kortrijk. 
