NUM'ART

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

**************************************************************************************************

 1= xy

Hyperbolic - Luc Janus

De vergelijking xy = 1 stelt in de vlakke (Euclidische) meetkunde een hyperbool voor.

Wiskundigen bedachten echter ook andere soorten meetkunde.

De schijf van Poincaré (google-opdracht voor wie hier meer wil over weten)
geeft bijvoorbeeld aanleiding tot een hyperbolische meetkunde.

**************************************************************************************************

 Een eenbladige hyperboloïde is een regeloppervlak.

Dit is een oppervlak waarbij door elk punt minstens één rechte (beschrijvende) gaat die volledig op het oppervlak ligt.

Op de onderstaande animatie kan je dit duidelijk zien.

Collega Jos Leys maakte me attent op het onderstaande filmpje. 
Het toont een experimentele opstelling in het Science Museum in Valencia
waarbij een rechte staaf blijkbaar probleemloos door een kromme opening gaat.
Zie je direct het verband met de hyperboloïde?

*************************************************************************************************

En mocht je nog niet helemaal overtuigd zijn ...

20-01-2015 om 00:00 geschreven door Luc Gheysens  

DE MAANILLUSIE

Sedert de oudheid hebben wetenschappers zoals Archimedes, Ptolemaeus, Leonardo Da Vinci en Descartes geprobeerd
een verklaring te vinden voor het feit dat de maan schijnbaar veel groter is wanneer ze dicht bij de horizon staat.
Verschillende foto's ‘bewijzen’ het bestaan van zo een 'supermaan'.

Volgens een recente theorie zou de illusie kunnen verklaard worden via convergence micropsia.
Met deze Engelse term duiden wetenschappers aan dat onze hersenen ons wijs maken
dat wanneer de maan dicht bij de horizon staat, ze ver van ons af staat en vrij groot is.
Wanneer ze echter hoog aan de hemel staat, 'zien' onze hersenen ze kleiner omdat ze denken dat ze dichterbij staat.
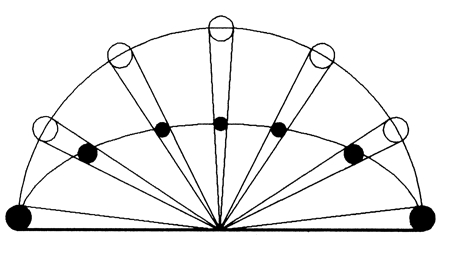
De onderstaande figuur verduidelijkt dit:
de witte cirkeltjes stellen de maan voor zoals ze werkelijk is
en de zwarte cirkeltjes hoe onze hersenen ze 'zien'.

    

Het volgende Youtubefilmpje behandelt dit merkwaardig fenomeen, waarover het laatste woord nog niet gezegd is.

**************************************************************************************************

Kan je nu ook het onderstaande 'maantjesprobleem' oplossen?

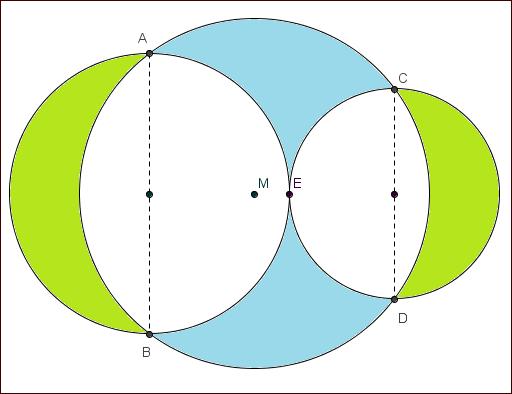
Twee cirkels raken elkaar uitwendig in een punt E.

[AB] en [CD] zijn middellijnen van deze twee cirkels die loodrecht staan op de rechte door hun middelpunten.

Een derde cirkel met middelpunt M gaat door de punten A, B, C en D.

Toon aan dat de oppervlakte van  de twee 'groene maantjes' gelijk is aan de oppervlakte van de twee 'blauwe maandelen'.

Oplossing in bijlage!

Bijlagen:
OPLOSSING VAN HET MAANTJESPROBLEEM.pdf (184.9 KB)   

3-6-9-12 First Impression - Luc Janus

De rij getallen 3, 6, 9, 12 heeft wel een bijzondere betekenis gekregen.

Voor de ene doen ze wellicht denken aan een klok en voor de andere misschien wel aan de vier seizoenen.

Luc Janus vertaalde hier beide associaties op een artistieke manier in twee prenten. 

3-6-9-12 Second Impression - Luc Janus

******************************************************************************************************************

Een leuke 3-6-9-12-vraag is de volgende: kan je een rechthoek vullen met

3 vierkanten van 3 op 3, 6 vierkanten van 6 op 6, 9 vierkanten van 9 op 9 en 12 vierkanten van 12 op 12?

      Yes, we can!

Bron: http://www2.stetson.edu/~efriedma/mathmagic/0106.html .

18-01-2015 om 00:00 geschreven door Luc Gheysens  

VIER KEER PI

Het bovenstaande 'Pi-ctogram' (een sangaku waarin pi de hoofdrol speelt)

is een uitnodiging voor een eenvoudige opgave.

Van een gelijkzijdige driehoek is de ingeschreven en de omgeschreven cirkel getekend.

Als de ingeschreven cirkel als oppervlakte π heeft, toon dan aan

dat de drie gebieden in dezelfde kleur eveneens als oppervlakte π hebben.

Tip. Bepaal de straal van de in- en de omgeschreven cirkel en dan is de opgave in één-twee-drie opgelost!

17-01-2015 om 00:00 geschreven door Luc Gheysens  

Daar heb je pi weer!

Bijlagen:
Pi bij rechthoekige driehoek en twee halve cirkels - oplossing.pdf (174.2 KB)   

TIENS!

Een regelmatige tienhoek is ingeschreven in een cirkel met straal R.

Als men een hoekpunt van deze tienhoek verbindt met het derde erop volgende hoekpunt

en dit zo steeds verder doet, bekomt men een stervormige tienhoek (zie figuur).

Als |AB| de lengte is van de zijde  van de regelmatige tienhoek en |CD| de lengte van de zijde van de stervormige tienhoek,

toon dan aan dat het verschil van deze lengten gelijk is aan de straal R van de cirkel,

m.a.w. toon aan dat |CD| – |AB| = R .

Tip voor de oplossing.

Toon aan dat ABDP en CPME parallellograms zijn.

Veel magische krachten zijn er verder niet nodig!

15-01-2015 om 00:00 geschreven door Luc Gheysens  

HET PROBLEEM VAN DE DRIE RAKENDE CIRKELS

Drie cirkels raken elkaar twee aan twee uitwendig en ze raken ook alle drie aan een rechte. 

Touching circles - Luc Janus

Bijlagen:
HET PROBLEEM VAN DE DRIE RAKENDE CIRKELS - opgelost.pdf (76.4 KB)   

Wat heb je nodig?

Een blad papier, een potlood, een geodriehoek, een schaar, post its in twee verschillende kleuren en wat wiskundig inzicht.
Teken een willekeurige driehoek en projecteer een hoekpunt op de overstaande zijde.
Die zijde wordt zo in twee lijnstukken verdeeld en samen met de twee andere zijden heb je dus vier lijnstukken.

Knip uit de eerste soort post its twee vierkanten waarvan de zijde even lang is als de twee kortste lijnstukken (roze)
en knip uit de andere soort post its eveneens twee vierkanten waarvan de zijde even lang is als de twee langste lijnstukken (blauw).
Je ziet het resultaat op de linkse figuur.

Plaats nu de twee kleinere vierkanten bovenop de twee grotere zoals op de rechtse figuur is aangegeven.

Kan je bewijzen dat de twee (blauwe) gebieden van de grotere vierkanten die niet bedekt zijn even groot zijn?

Tip. Pas de stelling van Pythagoras toe!

 Als je het niet ziet zitten, lees dan de bijlage!

Bijlagen:
SANGAKU MET POST ITS - oplossing.pdf (65.7 KB)   

Voor de twaalfde uitdaging nemen we nog eens een regelmatige twaalfhoek onder de loep.

Kan je bewijzen dat de drie aangeduide diagonalen in een regelmatige twaalfhoek door één punt gaan?

Tip voor een mogelijk bewijs met behulp van goniometrie.
Door een gepaste keuze van het assenstelsel hebben de zes eindpunten van de aangestipte diagonalen
de volgende coördinaten: (cos15°, ± sin 15°), (cos 45°, ± sin 45°) en (cos 105°, ± sin 105°).
Door gebruik te maken van de formules van Simpson kan je dan aantonen
dat twee van de diagonalen de volgende vergelijking hebben:

y = x – cos 15° + sin 15°   en y = -x + cos 15° – sin 15°. 
Hun snijpunt ligt op de rechte   en dat is precies de vergelijking van de derde diagonaal!

*****************************************************************************************************************************

Hieronder staat nog een 'bewijs zonder woorden'.
Bron: Proofs without words II, Roger B. Nelsen.
Met dank aan Prof. Hendrik Van Maldeghem (UGent).

Gezien?

12-01-2015 om 00:00 geschreven door Luc Gheysens  

DE RECHTHOEK VAN PASCAL

In de wiskundelessen komt (zeker in de sterk-wiskundige richtingen) de driehoek van Pascal aan bod.

De leerlingen ontdekken dat hierin de zogenaamde binomiaalcoëfficiënten staan.

Dit zijn de getallen die het aantal combinaties uitdrukken van p elementen uit een verzameling met n elementen:

Voor het aantal herhalingscombinaties van p elementen uit een verzameling met n elementen gebruikt men hetzelfde symbool met een streepje erbovenop.

De onderstaande formule drukt het verband uit tussen herhalingscombinaties en combinaties (zonder herhaling):

Hieronder staat een figuur die we voor de gelegenheid de rechthoek van Pascal noemen.

Bijlagen:
De rechthoek van Pascal - opgelost.pdf (211.1 KB)   

Bij de viering van 40 jaar VVWL in Gent herinnerde Prof. Hendrik Van Maldeghem me aan het volgende probleem.

In een vierkant tekent men een zo groot mogelijke regelmatige twaalfhoek (zie onderstaande figuur).

Bewijs dat de oppervlakte van de twaalfhoek gelijk is aan 75% van de oppervlakte van het vierkant.

Tip voor de oplossing: verdeel de twaalfhoek in 12 driehoeken en gebruik de formule 2 sin 15° cos 15° = sin 30° = ½ .

************************************************************************************************************************

Hieronder zie je een elegant 'bewijs zonder woorden'.

Bron: Proofs without words II, Roger B. Nelsen.

Gezien?

10-01-2015 om 00:00 geschreven door Luc Gheysens  

Op 6 december 2014 vierde de Vlaamse Vereniging van Wiskundeleraars haar 40-jarig bestaan.

Prof. Hendrik Van Maldeghem (UGent) schotelde het publiek bij die gelegenheid 40 problemen voor.

Enkele van die problemen hadden te maken met cirkels, zoals je op de onderstaand foto's kunt zien.

Hij vermeldde ook een leuke opdracht die verband houdt met de ingeschreven cirkel van een driehoek.

OPGAVE.

In de vier hoeken van een rechthoek met afmetingen 4x en 4y tekent men een rechthoekige driehoek met rechthoekszijden x en y.

Bij elk van deze driehoeken tekent men de ingeschreven cirkel (fig. 1) en de raaklijnen loodrecht op de zijden van de rechthoek (fig. 2).

Op die manier wordt een 'pad' afgetekend binnen de rechthoek (fig. 3).

Toon aan dat de oppervlakte van dit pad precies de helft is van de oppervlakte van de rechthoek.

 Tip voor de oplossing.

Volgens de formule die gisteren op mijn blog aan bod kwam, hebben de cirkels met straal r een diameter die gelijk is aan

09-01-2015 om 00:00 geschreven door Luc Gheysens  

Collega Odette De Meulemeester gaf me ooit een muntstuk van 1 Yuan, dat ze had meegebracht van een reis naar China.

Op de beeldzijde (links) staat een bloeiende chrysant en op de muntzijde (rechts) bemerk je het symbool π met een streepje erop.

Blijkbaar is dit Chinees voor 'munteenheid' (= 1 Yuan) (zie http://en.wiktionary.org/wiki/%E5%85%83 ).

Ook collega Dirk Huylebrouck maakt ons dit duidelijk via de onderstaande Facebookfoto (met dank!).

De diameter van de munt is (afgerond) 2 cm zodat de oppervlakte (ongeveer) π cm² is. Toeval???

En als kind leerde men me dat iemand met veel  πng-πng (lees: ping-ping) er warmpjes in zit!

Dit is meteen de aanleiding voor een eenvoudige wiskunde-oefening

 Oplossing in bijlage.

Bijlagen:
Eigenschap met pi - oplossing.pdf (82.1 KB)   

SANGAKU MET EEN RECHTHOEK,

EEN CIRKEL EN ZES VIERKANTEN

Neem een willekeurig punt op de omgeschreven cirkel van een rechthoek.

Verbind dit punt met de vier hoekpunten van de rechthoek.

De som van de oppervlakten van de vier vierkanten geconstrueerd op deze vier lijnstukken

is gelijk aan de som van de oppervlakten van de twee vierkanten geconstrueerd

op de diagonalen van de rechthoek.

Kan je dit aantonen?

Bijlagen:
SANGAKU MET EEN RECHTHOEK CIRKEL EN ZES VIERKANTEN - bewijs.pdf (115.3 KB)   

SANGAKU MET PYTHAGORESE CIRKELS

In een rechthoekige driehoek construeert men op de schuine zijde de rechthoek met de grootst mogelijke oppervlakte.

In de drie hoeken van de driehoek ontstaat zo een rechthoekig driehoekje.

De oppervlakte van de ingeschreven cirkel van het grootste driehoekje is dan gelijk

aan de som van de oppervlakten van de ingeschreven cirkels van de twee andere driehoekjes

Kan je dat bewijzen?

 Opmerking. De drie ingeschreven cirkels noemen we daarom Pythagorese cirkels.

En ja, de drie koningen hebben het vandaag te druk om je te helpen bij het bewijs.

Zelf zoeken is dus de boodschap (of direct de bijlage openen)!

Collega Wim Haazen (lees hieronder zijn reactie) zorgde zelfs voor een knap en kort bewijs. Merci beaucoup!

Hallo Luc,

Aangezien de opp. van de driehoek  met de rode cirkel ¼ deel is van de grote driehoek,
en de geconstrueerde rechthoek de helft is van de driehoek
geldt natuurlijk dat de som van de oppervlaktes van de driehoeken met de groene cirkels gelijk is aan de oppervlakte van de driehoek met de rode cirkel
en aangezien de driehoeken allemaal gelijkvormig zijn,
geldt dat ook voor hun ingeschreven cirkels.

Groeten, Wim Haazen, Venlo

Bijlagen:
SANGAKU MET PYTHAGORESE CIRKELS - oplossing.pdf (239.6 KB)   

PI-SANGAKU 

In een cirkel met diameter 10 zijn zes cirkels beschreven zoals op de bovenstaande figuur is aangegeven.

Kan je aantonen dat de oppervlakte van de kleine cirkel gelijk is aan π?

Oplossing in bijlage!

En heb je reeds een stelletje pi-potloden besteld?

Ik heb de mijne alvast als nieuwjaarsgeschenk gekregen!     

Op de potloden staat het getal pi met 95 cijfers na de komma afgedrukt.

Info op https://www.etsy.com/nl/listing/66937949/the-pi-pencil-to-96-digits-6-pack-look

Bijlagen:
PI-SANGAKU opgelost.pdf (226.3 KB)   

You are so square - Luc Janus

SANGAKU MET 2 + 0 – 1 + 5 VIERKANTEN

Projecteer een willekeurig punt binnen een willekeurige driehoek op de drie zijden van de driehoek.
Elke zijde wordt zo verdeeld in twee stukken.
Construeer een vierkant op elk van de zes lijnstukken.
Dan is de som van de oppervlakte van de drie rode vierkanten gelijk aan
de som van de oppervlakten van de drie groene vierkanten.

Kan je dat bewijzen?

Tip. Blijf kalm en pas de stelling van Pythagoras toe.

 Of  als je frustraties wilt vermijden:  kijk direct naar het bewijs in de bijlage.

Bijlagen:
SANGAKU met zes vierkanten - bewijs.pdf (176.8 KB)   

DE EERSTE LEUKE SANGAKU VAN 2015

Op de bovenstaande figuur bemerk je een rechthoek en een vierkant die dezelfde oppervlakte hebben.

De zijde van het vierkant is het lijnstuk dat een gemeenschappelijke raaklijn aan beide cirkels bepaalt.

De lengte en de breedte van de rechthoek zijn precies de diameters van beide cirkels.

Kan je dit ook bewijzen?

Misschien kan het bewijs in bijlage je toch nog een vrolijke dag bezorgen !?

Bijlagen:
SANGAKU met cirkels en vierkant en rechthoek - oplossing.pdf (129.6 KB)   

DE STELLING VAN DE VIJF VIERKANTEN

Op vier zijden van een parallellogram construeert men naar buiten toe een vierkant.

Dan zijn de middelpunten van deze vier vierkanten de hoekpunten van een vierkant.

Tips voor het bewijs zitten in de bijlage.

Met behulp van de cosinusregel kan je bovendien aantonen
dat de oppervlakte van het grootste vierkant gelijk is aan
de oppervlakte van het parallellogram vermeerderd
met de helft van de oppervlakte van elk van de twee soorten kleinere vierkanten!

*******************************************************************************************

Tip voor wie denkt in 2015 in financiële problemen te komen:
deze smartphone is nu te koop op www.alibaba.com.

Bijlagen:
DE STELLING VAN DE VIJF VIERKANTEN - bewijs.pdf (174 KB)   

Met al mijn goede wensen voor het nieuwe jaar!

Feeling hap-pi - Luc Janus

Ziehier een eerste wiskundige uitdaging voor 2015.

En dan duikt π weer op.

Kan je aantonen dat de beide gekleurde gebieden op de onderstaande figuur π als oppervlakte hebben?

De lengte van de twee rechthoekszijden kan je aflezen op de figuur.



 

Wie deze uitdaging op 1 januari nog wat te zwaar vindt, verwijs ik graag naar de bijlage.

Bijlagen:
SANGAKU MET VIJF HALVE CIRKELS - oplossing.pdf (223.7 KB)