100 DAGEN

OF

VAN CHRYSOSTOMOS TOT ALLE REMMEN LOS

Foto's: De Bron - Tielt

07-03-2015 om 00:00 geschreven door Luc Gheysens  

Zonsverduistering op 20 maart 2015

Over 14 dagen, op vrijdag 20 maart 2015, tussen 09:30 uur en 11:48 uur, vindt een gedeeltelijke zonsverduistering plaats.

Bij helder weer zal deze zonsverduistering vanuit Nederland en België goed zichtbaar zijn.

Tijdens het maximum, om 10:37 uur, zal 81% van haar oppervlakte bedekt zijn.

Bijlagen:
OPGAVE OVER ZONSVERDUISTERING - oplossing.pdf (183.5 KB)   

HET PROBLEEM VAN DE UITGEKNIPTE VIERKANTEN

Δ ABC is een willekeurige driehoek.
Op de zijde [BC] construeert men buiten de driehoek  het vierkant BCNM.
Met [AM] en [AN] als zijden construeert men daarna twee vierkanten zoals op de figuur.
Uit het vierkant met zijde [AM] knipt men een vierkant weg waarvan de zijden lengte c = |AB| hebben
en uit het vierkant met zijde [AN] knipt men een vierkant weg waarvan de zijden lengte b = |AC| hebben.

Toon aan dat de resterende (blauwe) stukken van beide vierkanten dezelfde oppervlakte hebben.

En misschien vind je in een collega wel de geknipte persoon om je helpen bij vinden van een bewijs!

Of lees direct de bijlage.

Bijlagen:
PROBLEEM VAN DE VERKNIPTE VIERKANTEN - opgelost.pdf (184.6 KB)   

DE MUMMIE VAN PINEDJEM

Pinedjem II (ook wel Pinudjem II genoemd) was een hogepriester in het Oude Egypte van rond 1000 v. Chr.
Hij was gehuwd met zijn zuster met wie hij drie kinderen had en met zijn nicht met wie hij vier kinderen had.

Op de bovenstaande figuur staat niet de mummie van Pinedjem afgebeeld, maar een shabti.

Een shabti is een beeldje dat de overledene in het Oude Egypte meenam in zijn graf om voor hem in het Dodenrijk het werk te verrichten.
Het woord 'shabti' betekent 'antwoorder', namelijk als de overledene werd geroepen,
dan moest het grafbeeldje als plaatsvervanger antwoorden.
De grafbeeldjes werden voornamelijk van hout, steen of faience gemaakt en varieerden in grootte. 
(Bron: wikipedia, met dank aan Peter Raedschelders).

De gekruiste armen van het beeldje maken hoeken van 15° met de basis van de gelijkzijdige driehoek.
Stel dat de zijden van de gelijkzijdige driehoek lengte   hebben.
En stel dat de top van die driehoek en de top van de gelijkbenige driehoek met basishoeken van 15°
een middellijn bepalen van de afgebeelde cirkel.

Kan je dan aantonen dat de oppervlakte van de cirkel gelijk is aan π? 

Oplossing in bijlage.

Bijlagen:
DE MUMMIE VAN PINUDJEM - opgelost.pdf (294.2 KB)   

PI BIJ CIRKEL EN ELLIPS

03-03-2015 om 00:00 geschreven door Luc Gheysens  

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

PS. Vandaag is het toevallig ook 2/3 of 2 maart.

************************************************************

2/3

3M - Luc Janus

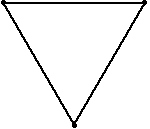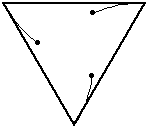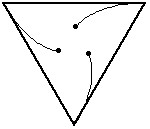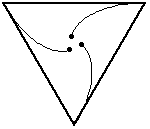
Drie muizen bevinden zich op de hoekpunten van een gelijkzijdige driehoek.

De zijden van de driehoek zijn 1 meter lang.

Elke muis loopt naar de muis toe die zich aan haar rechterzijde bevindt

en dus zelf ook naar de muis aan haar rechterzijde toeloopt.

De muizen zullen elkaar ontmoeten in het zwaartepunt van de driehoek

nadat ze een afstand van 0,666... of 2/3 meter hebben afgelegd.

Meer uitleg op http://mathworld.wolfram.com/MiceProblem.html .

*********************************************************************

3M verwijst hier niet alleen voor '3 Muizen'

maar 3M (Minnesota Mining and Manufacturing Company) is ook de firma die de post-its op de markt bracht.

Hieronder zie je hoe een kunstenaar Marilyn Monroe te voorschijn toverde met behulp van post-its.

Of die kunstenaar een bril droeg weet ik niet...

02-03-2015 om 00:00 geschreven door Luc Gheysens  

DE RECTIFICATIE VAN KOCHANSKI

Rekenwerk in bijlage!

Bijlagen:
DE RECTIFICATIE VAN KOCHANSKI.pdf (214.2 KB)   

HET PROBLEEM VAN DE PYGMEEËN

Een groep pygmeekinderen ging in een cirkel zitten met de voetjes mooi tegen elkaar;

Een fotograaf legde dit beeld vast. De pygmeeën konden echter niet begrijpen dat hun voetjes op de foto een ellips vormden.

Als jij ooit van affiene meetkunde hebt gehoord, dan kan je dat zeker verklaren!

******************************************************************************************************

In dit verband vermelden we hier een eenvoudig meetkundeprobleem met een cirkel en een ellips.

 Gegeven: een cirkel met middelpunt O(0,0) en straal r = 10 en een vast punt F(8,0) .

Bijlagen:
HET PROBLEEM VAN DE PYGMEEËN - opgelost.pdf (137.9 KB)   

SANGAKU MET VIJF EVEN GROTE VIERKANTEN

     

Δ ABC is een willekeurige driehoek en M is het midden van de zijde [BC].

Op de zijden [AB] en [AC] construeert men de vierkanten ABDE en ACGF buiten de driehoek ABC.

Toon aan dat het vierkant met [EF] als zijde vier keer zo groot is als het vierkant met [AM] als zijde.

 Op de rechtse figuur staan alle punten aangeduid en wie het bewijs niet direct ziet zitten, vindt hieronder een tip voor de oplossing.

Verleng [AM] zodat |AA'| = 2|AM| en toon dan aan dat Δ ABA' congruent is met Δ EAF.

De uitwerking vind je in de bijlage.

Bijlagen:
SANGAKU MET VIJF EVEN GROTE VIERKANTEN - opgelost.pdf (196.4 KB)   

SANGAKU MET KOORDENVIERHOEKEN

De afstand van een punt van een cirkel tot een koorde is middelevenredig

tussen de afstanden van dat punt tot de raaklijnen in de eindpunten van die koorde.

Als je dit kunt bewijzen, dan heb je meteen aangetoond dat de rechthoek en het vierkant op de figuur dezelfde oppervlakte hebben!

En heb je ook gezien waar de twee koordenvierhoeken in de figuur verscholen zitten?

Oplossing in bijlage (met dank aan collega Wim Haazen, Venlo).

Bijlagen:
SANGAKU MET KOORDENVIERHOEKEN opgelost.pdf (186 KB)   

EEN KOORDENVIERHOEK EN TWEE RECHTHOEKEN

ABCD is een koordenvierhoek en P is een willekeurig punt op de omgeschreven cirkel.

De afstanden van P tot twee overstaande zijden van ABCD zijn a en c en tot de twee andere overstaande zijden b en d.

Te bewijzen: ac = bd.

En da's nu eens een niet zo eenvoudige opgave !

MORE BRAINS ARE NEEDED

OPLOSSING IN BIJLAGE

Bijlagen:
Een koordenvierhoek en twee even grote rechthoeken - opgelost.pdf (289.2 KB)   

NUM'ART is een artistiek project bedacht door Luc Janus.

Hij zet hierbij elke week een getal op een artistieke manier in de kijker.

****************************************************************************

2525

If man is still alive - Luc Janus

****************************************************************************************  

In the year 2525 werd in 1969 een wereldhit
voor het Amerikaanse pop-rockduo Zager en Evans.

Reeds in 1968 werd deze song als themalied gebruikt
voor de Vietnamfilm Tunnel Rats.

*******************************************************************************************
WEETJE

Weet jij het antwoord op de volgende VWO-vraag (Eerste ronde 1990-1991)?

© Vlaamse Wiskunde Olympiade v.z.w.

24-02-2015 om 00:00 geschreven door Luc Gheysens  

SANGAKU MET EEN WONDERBARE KOORDE

Een koorde [AB] snijdt een middellijn van een cirkel met straal r in een punt P onder een hoek van 45°.

Te bewijzen: |PA|² + |PB|² = 2r².

Zie je dat zitten???

Drie verschillende bewijzen vind je in bijlage.

Bijlagen:
DE WONDERBARE KOORDE opgelost.pdf (260 KB)   

EVEN GROTE DRIEHOEKEN

Naar aanleiding van het probleem met de twee even grote rechthoeken in een gelijkbenige driehoek dat hier gisteren verscheen,
bezorgde ere-collega Noud Meelen uit het Nederlandse Noord-Brabant me de onderstaande GeoGebra-tekening.
De figuur bevat een mooi BEWIJS ZONDER WOORDEN
voor het feit dat er op de tekening twee even grote (witte) rechthoeken staan.

Merci!

Kan je BEWIJZEN MET WOORDEN dat de driehoeken in dezelfde kleur even groot zijn?

23-02-2015 om 00:00 geschreven door Luc Gheysens  

Tip voor het bewijs. Δ EMB is gelijkvormig met  Δ FNC.

En als je hiermee nog niet direct het licht ziet, lees dan de bijlage.

Bijlagen:
EVEN GROTE RECHTHOEKEN IN EEN GELIJKBENIGE DRIEHOEK - oplossing.pdf (166.2 KB)   

PIPO DE CLOWN

Hoe teken je het hoofd (met hoedje) van Pipo de Clown?

Begin met een gelijkzijdige driehoek ABC te tekenen

en teken daarin de cirkel die in B en C raakt aan de zijden [AB] en [AC].

Gebruik daarna jouw fantasie ...  

Als de zijden van de driehoek als lengte √3  hebben, dan is de oppervlakte van de cirkel gelijk aan π. 

Kan je dit bewijzen?

TIP. Cosinusregel in Δ MBC  met M het middelpunt van de cirkel.

ANDERE TIP. tan 30° in Δ ABM met M het middelpunt van de cirkel.

21-02-2015 om 00:00 geschreven door Luc Gheysens  

MACHTIGE SANGAKU

Waarom hebben de rechthoek en het vierkant dezelfde oppervlakte?

Hieronder zie je de verklaring!

20-02-2015 om 00:00 geschreven door Luc Gheysens  

ZESTIGPLUSSERS IN HET ONDERWIJS

Uit het jaarrapport ‘Ziekteverzuim van het Vlaamse Onderwijspersoneel’

blijkt dat de West-Vlaamse leerkrachten het minst vaak ziek zijn.

Uit dit rapport blijkt ook dat vooral zestigplussers in de nabije toekomst met het burn-out-probleem zullen moeten afrekenen ...

Het getal 60 (zestigplussers) en de cirkeltjes op de rechtse afbeelding met ongeveer 1% en 9% inspireerden me tot een nieuwe pi-sangaku.

************************************************************************************************************************

NIEUWE PI-SANGAKU

De twee raaklijnen uit een punt aan een cirkel met oppervlakte 9π vormen een hoek van 60°.

Een kleinere cirkel raakt uitwendig aan deze cirkel en aan die twee raaklijnen.

Te bewijzen:  de oppervlakte van de kleine cirkel is π.

DOORDENKERTJE

Als leraren nu per week 20 lesuren geven, zijn dat in feite 20 lessen van 50 minuten en 20 x (50/60) = 16,67 uren .

Een dag voor een leerkracht telt dus 24 x (60/50) = 28,8 uren.

Ligt hier verklaring van stress en het burn-out-effect in het onderwijs?

Bijlagen:
NIEUWE PI-SANGAKU opgelost.pdf (288.4 KB)   

GONIOMETRIE EN PI

Enkele tips voor de oplossing. 

Gebruik de definitie van sinus van een scherpe hoek in een rechthoekige driehoek.

Denk eraan:  sin 75° = cos 15° en 2 sin 15° cos 15° = sin 30°  = ½ .

Hiermee is het bewijs wellicht eenvoudiger dan een pirouette!

In bijlage zit nog een a-goniometrisch bewijs.

Bijlagen:
A-goniometrisch bewijs.pdf (172.3 KB)   

HELIX

Een helix (van het Griekse έλιξ = gedraaid) of schroeflijn is een drie-dimensionale spiraalachtige figuur.

Een schroeflijn bevindt zich in feite op een cilinder en je treft ze aan op een boor, op een kurkentrekker, op vijzen ...

De afstand tussen twee windingen in de richting van de as van de cilinder gemeten noemt men de spoed van de schroeflijn.

Op de onderstaande figuur is de afstand tussen de punten A en B de spoed van de afgebeelde helix.

*****************************************************************************************

Beschouw de schroeflijn die bepaald is door de volgende cartesische coördinaten:

.

De schroeflijn bevindt zich op een cilinder met straal r = 0,4.

Het beginpunt (voor t = 0) is A(2/5, 0, 0) en na één volledige omwenteling (t = 2π) vinden we het punt B(2/5, 0, 3π/5).

Kan je bewijzen dat de lengte van de schroeflijn tussen A en B gelijk is aan π?

Wie niet direct een oplossing vindt, verwijzen we - met de glimlach - door naar de bijlage!

Bijlagen:
LENGTE VAN EEN SCHROEFLIJN.pdf (201.1 KB)