|
TOPOLOGIE
In mijn studententijd was TOPOLOGIE een belangrijk wiskundige studieonderwerp
dat je zelfs in de leerplannen van het secundair onderwijs tegenkwam.
Topologie is een tak van wiskunde die zich bezighoudt met eigenschappen van objecten die onveranderd blijven bij vervorming:
uitrekken, draaien, pletten alles mag zolang ze maar niet scheuren of anderszins kapot gaan.
De grootte van een voorwerp doet dus in de topologie niet ter zake.
Wel hoeveel gaten er in zitten, of het begrensd is, en het aantal dimensies.
Twee oppervlakken heten homeomorf als het ene oppervlak via een continue vervorming te verkrijgen is uit het andere.
Wiskundigen leggen het vaak uit aan de hand van koffiekopjes en donuts:
het onderstaande plaatje laat zien dat het oppervlak van een koffiekop en dat van een donut homeomorf zijn.

Een koffiekop en een donut zijn homeomorf: de ene is via een continue vervorming te transformeren in de andere.
Een topoloog bestudeert geen koffiekopjes en donuts.
Die voorwerpen gebruiken ze alleen om uit te kunnen leggen waar ze zich ongeveer mee bezig houden.
Het gaat om abstracte vormen, waarbij het aantal dimensies gerust meer dan drie mag zijn.
Via het onderstaande applet kan je deze vervorming 'live' meemaken.

GRAFENTHEORIE
In de grafentheorie is het probleem van de zeven bruggen van Koningsbergen voor het eerst opgelost door Leonhard Euler in 1736.
De zeven bruggen van Koningsbergen.
In de geschiedenis van de wiskunde is het één van de eerste grafentheoretische problemen.
Omdat de grafentheorie als een deelveld van de topologie kan worden beschouwd
vormt dit vraagstuk ook een van de eerste problemen binnen de topologie die formeel geanalyseerd zijn.
De stad Koningsbergen (heden ten dage Kaliningrad) lag in het oosten van Pruisen aan de rivier de Pregel,
waarin twee eilanden lagen die door zeven bruggen met elkaar en met de vaste wal verbonden waren;
dit staat hieronder schematisch afgebeeld.
De vraag was nu of het mogelijk is om zó te wandelen dat je precies één maal over elke brug loopt en weer op je beginpunt eindigt.
In 1736 heeft Euler aangetoond dat dit onmogelijk is.
Tevens heeft hij laten zien dat het probleem beschouwd kan worden als een probleem op een graaf,
waarin het vraagstuk over de bruggen van Koningsbergen als volgt geabstraheerd is:

In de graaf, de rechter afbeelding, wordt elke brug voorgesteld door een lijn, en de eilanden en oevers door een blauw knooppunt.
De punten die aan een oneven aantal lijnen grenzen, noemen we punten van oneven graad.
In de bovenstaande graaf zijn dus alle punten van oneven graad
(in één punt komen vijf lijnen samen en in de drie andere punten telkens drie lijnen).
Om een Eulerwandeling of Eulertoer, waarbij men precies één keer over elke lijn loopt,
mogelijk te maken, moeten er nul of twee punten van oneven graad zijn.
Zijn er twee punten van oneven graad, dan moet de wandeling starten in het ene oneven punt en eindigen in het andere oneven punt.
Zijn er geen punten van oneven graad, dan kan de wandeling overal beginnen en eindigt de wandeling waar hij begonnen is.
Het is dus onmogelijk om een Eulerwandeling over de bruggen Koningsbergen te maken
omdat de vier knooppunten van oneven graad zijn.
Het verschil tussen de echte ligging en de schematische weergave van hierboven
is een goed voorbeeld van het kenmerk dat topologie zich niet bezighoudt met de exacte weergave van zaken,
maar meer met hun relatieve vorm.
Bron: wikipedia.
Een bekend puzzeltje bestaat er in om een bepaalde figuur te tekenen zonder het potlood van het papier te nemen.
Je mag ook maar één keer over elke lijn gaan.
Dat puzzeltje is oplosbaar als er hoogstens twee punten zijn waarin een oneven aantal lijnen samenkomt.
Men moet dan in een van die punten beginnen.
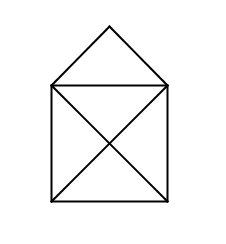
Kan je het onderstaande huisje in één trek tekenen?
27-01-2012 om 00:00
geschreven door Luc Gheysens 
|
